Suchergebnis
vom: 20.01.2015
Bundesministerium für Umwelt, Naturschutz, Bau und Reaktorsicherheit
BAnz AT 17.04.2015 B2
Bundesministerium
für Umwelt, Naturschutz, Bau und Reaktorsicherheit
Bekanntmachung
einer Stellungnahme mit wissenschaftlicher
Begründung der Strahlenschutzkommission
(Einflussfaktoren auf das Geschlechtsverhältnis
der Neugeborenen unter besonderer Betrachtung
der Wirkung ionisierender Strahlung – vom 17. Juli 2014)
Nachfolgend wird die Stellungnahme nebst wissenschaftlicher Begründung der Strahlenschutzkommission (SSK), verabschiedet in der 270. Sitzung der Kommission am 17./18. Juli 2014, bekannt gegeben.
RS II 2 - 17027/2
Bundesministerium
für Umwelt, Naturschutz, Bau und Reaktorsicherheit
Dr. Helming
Einflussfaktoren auf das Geschlechtsverhältnis der Neugeborenen
unter besonderer Beachtung der Wirkung ionisierender Strahlung
Stellungnahme der Strahlenschutzkommission mit wissenschaftlicher Begründung
Verabschiedet in der 270. Sitzung der Strahlenschutzkommission am 17./18. Juli 2014
Inhaltsübersicht
I Stellungnahme der Strahlenschutzkommission
II Wissenschaftliche Begründung
1 Einleitung
2 Auswirkungen von Definitionsänderungen auf das Geschlechtsverhältnis von Neugeborenen
2.1 Abgrenzung von Lebend-, Tot- und Fehlgeburten
2.2 Auswirkungen auf demografische Ziffern
2.3 Auswirkungen auf das Geschlechtsverhältnis
3 Beispiele aus der Epidemiologie
3.1 Trends des Geschlechtsverhältnisses
3.2 Ländervergleiche
3.3 Alter der Eltern und Geburtsreihenfolge
3.4 Assistierte Reproduktion
3.5 Frühgeburten und Totgeburten
3.6 Zeitreihenbetrachtungen in Deutschland seit 1946
4 Studien zu ionisierender Strahlung
4.1 Atombombenüberlebende von Hiroshima und Nagasaki
4.2 Beschäftigte in britischen kerntechnischen Anlagen
4.2.1 Sellafield
4.2.2 Andere Anlagen
4.3 Bewohner der Umgebung des Atomwaffentestgeländes in Kasachstan
4.4 Übersicht über die erwähnten und weitere Studien
4.5 Biologischer Aspekt
4.6 Zusammenfassung
5 Methodische Bedingungen
5.1 Untersuchungen an Tieren und Vergleiche mit Studien am Menschen
6 Zusammenfassung und Schlussfolgerungen
7 Literatur
Anhang
I Stellungnahme der Strahlenschutzkommission
Mit dem Beginn bevölkerungsstatistischer Messungen wurde dem Anteil der Knaben- bzw. Mädchengeburten an allen neugeborenen Kindern eine hohe Aufmerksamkeit gewidmet. Dabei zeigte sich, dass im Schnitt etwa 1 050 bis 1 060 Knabengeburten auf 1 000 Mädchengeburten kommen. Das Geschlechtsverhältnis könnte prinzipiell außer durch endogene Faktoren, wie Alter und genetische Disposition, von einer Vielzahl von Faktoren, wie dem Lebensstil (z. B. der Ernährung), dem Sexualverhalten, der Familienplanung und der Umwelt beeinflusst sein. Von einzelnen Wissenschaftlern wurde in den letzten Jahren erneut die Exposition gegenüber ionisierender Strahlung ins Gespräch gebracht (z. B. Scherb und Voigt 2011). Dies ist Anlass für diese grundsätzliche Stellungnahme der Strahlenschutzkommission (SSK) zu den wissenschaftlichen Untersuchungsergebnissen bezüglich der Einflussfaktoren auf das Geschlechtsverhältnis der Neugeborenen.
Diese Stellungnahme stellt die Komplexität des Problems dar, geht auf die wichtigsten diskutierten Faktoren ein, zeigt die methodischen Schwierigkeiten auf, macht deutlich, dass es zu keinem Faktor eine befriedigende wissenschaftliche Erklärung gibt, und muss daher grundsätzlich bleiben. Insbesondere wird die Problematik der selektiven Abtreibungen, die für einzelne Länder den wesentlichsten Faktor darstellen, in der vorliegenden Stellungnahme bei der Betrachtung des Geschlechtsverhältnisses nicht berücksichtigt.
Aufgrund der in der wissenschaftlichen Begründung dargelegten Analysen und Betrachtungen kommt die SSK zu folgender Stellungnahme:
- 1.
-
Die Variation des Geschlechtsverhältnisses der Neugeborenen ist ein aus wissenschaftlicher Sicht hoch interessantes Phänomen. Dies zeigt sich in vielfältigen Publikationen aus unterschiedlichen Wissenschaftsbereichen.
- 2.
-
Am ehesten erscheint eine Verschiebung des Geschlechtsverhältnisses hin zu einem größeren Anteil von Knabengeburten in Zeiten wirtschaftlicher Instabilität und Krieg gesichert, ohne dass die dahinterliegenden Kausalfaktoren auch nur ansatzweise verstanden wären.
- 3.
-
Die Anwendung komplizierterer ausschließlich statistischer Verfahren auf die Analyse des Geschlechtsverhältnisses der Lebendgeborenen lässt keinerlei Erkenntnisfortschritt erwarten, da die komplexen Ursache-Wirkungs-Mechanismen aufgrund der Datenlage nicht weiter aufgeschlüsselt werden können.
Die SSK stellt fest, dass es bisher keine überzeugende konsistente wissenschaftliche Evidenz für die bislang betrachteten möglichen Einflussfaktoren, wie endogene und exogene Faktoren, gibt. Dies gilt insbesondere auch für ionisierende Strahlung.
II Wissenschaftliche Begründung
1 Einleitung
Mit dem Beginn bevölkerungsstatistischer Messungen wurde dem Anteil der Knaben- bzw. Mädchengeburten an allen neugeborenen Kindern eine hohe Aufmerksamkeit gewidmet. Dabei zeigte sich, dass im Schnitt etwa 1 050 bis 1 060 Knabengeburten auf 1 000 Mädchengeburten kommen (Jöckel und Pflaumer 1981). Der berühmte Demograf J. P. Süßmilch (Süßmilch 1765, S. 246) erblickte in diesem Knabenüberschuss einen göttlichen Willen und formulierte „Der weiseste Schöpfer hat in der Natur dieses Gesetz der Ordnung festgestellt, dass im Ganzen und Grossen jederzeit mehr Knaben als Mädchen gebohren werden, und zwar ist dieses Gesetz so genau bestimmet und so bewunderungswürdig eingeschränket, daß im Grossen allezeit und überall gegen 20 Töchter 21 Söhne gebohren werden, oder gegen 25 Töchter 26 Söhne, welches einerley ist, es werden allezeit aufs Hundert 4 bis 5 Söhne mehr, als Töchter, gebohren; selten 3 und 6 aufs 100, noch seltener aber 7 bis 8 aufs Hundert.“, um dann an anderer Stelle auf die erhöhte Sterblichkeit des männlichen Geschlechts, u. a. durch Kriege hinzuweisen. In und nach Kriegs- und Notzeiten war dieses Geschlechtsverhältnis (engl. sex ratio bzw. sex odds) sogar häufig zu einem noch deutlich größeren Anteil von Knabengeburten hin verschoben (Jöckel und Pflaumer 1981). Seitdem haben sich immer wieder Wissenschaftler aller Disziplinen bemüht, Determinanten für das Geschlechtsverhältnis der Lebendgeborenen, also das Verhältnis von Knaben- zu Mädchengeburten, zu ermitteln. Denn eines stand relativ schnell fest: Auch wenn ein „Knabenüberschuss“ von 50 bis 60 auf 1 000 Mädchengeburten nahezu eine Naturkonstante zu sein scheint, so verhalten sich die beobachteten realen statistischen Zahlen nicht so, als wenn das männliche Geschlecht mit einer verfälschten Münze im Verhältnis 1 050/2 050 = 51,2 % oder 1 060/2 060 = 51,5 % oder einer anderen Wahrscheinlichkeit p > 50 % „ausgewürfelt“ würde. Vielmehr zeigten sich „Extravariation1“, Schwankungen im Jahresverlauf und mit Not- und Kriegszeiten sowie anderen Faktoren assoziierte Niveauveränderungen (Mathews und Hamilton 2005, Davis et al. 1998). Statistisch gesprochen, ist die Annahme einer Binomialverteilung für den Anteil der Knabengeburten nicht vertretbar.
Es verwundert daher nicht, dass neben Determinanten bzw. (mit)verursachenden Faktoren, wie Elemente des Lebensstils (wie Ernährung), des Sexualverhaltens, der Umwelt, von einzelnen Wissenschaftlern auch die Exposition gegenüber ionisierender Strahlung angeboten wurde (Scherb und Voigt 2011). Letzteres war Anlass für diese eher grundsätzliche Stellungnahme der SSK zu den wissenschaftlichen Untersuchungsergebnissen bezüglich der Einflussfaktoren auf das Geschlechtsverhältnis der Neugeborenen. Diese Stellungnahme muss grundsätzlich bleiben, da die Breite der bislang erschienenen Veröffentlichungen zu diesem Thema, aber auch die lange Zeit, in der sich Wissenschaftler aus den unterschiedlichsten Perspektiven mit diesem Thema beschäftigt haben, eine umfassende Aufarbeitung aller Aspekte nicht zulassen. Insbesondere wird die Problematik der selektiven Abtreibungen, die für einzelne Länder den wesentlichsten Faktor darstellt, in der vorliegenden Stellungnahme bei der Betrachtung des Geschlechtsverhältnisses nicht berücksichtigt.
Einordnung der Thematik
Wenn wir über das Geschlechtsverhältnis der Lebendgeborenen reden, dann sprechen wir über eine statistische Maßzahl, die in einer Studie oder in der Bevölkerung nach der Geburt bestimmt wird. Die Faktoren, die diese Maßzahl bestimmen, wirken aber in aller Regel vor der Geburt. Die nachfolgende schematische Darstellung (Abbildung 1) macht dieses deutlich.
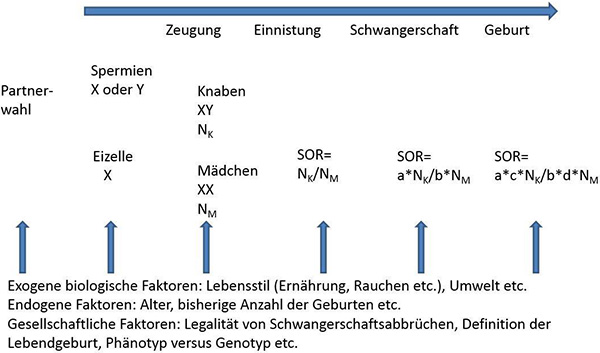
- Abb. 1:
-
Schematische Darstellung der Einwirkungsmöglichkeiten unterschiedlicher Faktoren auf das Geschlechtsverhältnis der Lebendgeborenen
- (1-a)
-
Anteil der Spontanaborte, induzierten Aborte und Fehlgeburten bei Knaben
- (1-b)
-
Anteil der Spontanaborte, induzierten Aborte und Fehlgeburten bei Mädchen
- (1-c)
-
Anteil der Totgeburten bei Knaben
- (1-d)
-
Anteil der Totgeburten bei Mädchen
- NK
-
Anzahl gezeugter Knaben
- NM
-
Anzahl gezeugter Mädchen
- SOR
-
Chancenverhältnis Knaben zu Mädchen
Will man die Wirkung eines bestimmten Faktors, z. B. der Ernährung, untersuchen bzw. bewerten, darf und muss man davon ausgehen, dass dieser Faktor potentiell Wirkungen auf jeder der in der Abbildung 1 gezeigten Stufen entfalten kann. Dabei können diese Wirkungen sowohl direkt als auch indirekt sein. So könnte die Art der Ernährung sowohl die Motilität der Spermien (direkte Wirkung) als auch das Sexualverhalten (indirekte Wirkung) beeinflussen. Außerdem ist eine gleichzeitige Wirkung auf anderen Stufen etwa durch eine veränderte Spontanabortrate vorstellbar. Neben diesem komplexen Ursachengeflecht gibt es die Ebene der gesellschaftlichen Beeinflussbarkeit des Gesamtgeschehens z. B. durch die Möglichkeit legaler Schwangerschaftsabbrüche, die selber wiederum mit der sozialen Lage (und damit auch mit Ernährungsfaktoren) assoziiert sein können.
In der Regel unterliegt bei Studien an Menschen der Endpunkt „Geschlechtsverhältnis“ legalen und statistischen Definitionserfordernissen. Dies bedingt jedoch in solchen Studien auch Fehler, die aufgrund von möglicherweise fehlerhaften Zuordnungen zu definierten Kategorien entstehen.
Fehler dieser Art können zu schwerwiegenden Interpretationsirrtümern führen, wie das folgende Beispiel zeigt. Im Jahr 2011 veröffentlichten Venero Fernández et al. im American Journal of Epidemiology (AJE) Daten zum Geschlechtsverhältnis der Lebendgeborenen aus Kuba, bei denen sich Mitte der 1990er Jahre ein Spitzenwert von 1 180 Knabengeburten auf 1 000 Mädchengeburten ergab. Die Autoren brachten dies in Zusammenhang mit der in Kuba durch den Zusammenbruch der Sowjetunion in den 1990er Jahren grassierenden Wirtschaftsdepression und der daraus resultierenden Mangelsituation der Bevölkerung. Am 7. Oktober 2012 schreibt die taz über die „kubanische Mädchenlücke“ (Kriener 2012) und bringt diese exorbitante Steigerung des Geschlechtsverhältnisses in Zusammenhang mit der angeblichen Lieferung radioaktiv verseuchter Lebensmittel nach dem Tschernobyl-Unfall aus der russischen Föderation nach Kuba. Es wird behauptet, dass diese kubanische Mädchenlücke inzwischen auch „in anderen medizinischen Fachblättern“ diskutiert würde. Eine Recherche in ISI Web of Science ergibt als Nachweis zu der Originalarbeit einen Brief an den Herausgeber des AJE bereits aus dem März des Jahres 2012 (Simpson 2012), nach dem es sich bei dem angeblichen Anstieg des Geschlechtsverhältnisses um ein rein statistisches Artefakt handelt, bei dem aufgrund der ökonomischen Mangelsituation keine korrekten Durchschreibebögen mehr verfügbar waren und diese durch eine „Billigvariante“ ersetzt werden mussten. Diese Billigvariante führte leider dazu, dass Mädchen in der offiziellen Statistik fälschlicherweise als Jungen (durch Verrücken der Kategorie im Durchschreibeverfahren) registriert wurden. Den Autoren des initialen Artikels blieb damit keine andere Möglichkeit, als diese, anders als ursprünglich gedachte, Erklärungsalternative zu akzeptieren (Venero Fernández et al. 2012). Nicht eine biologische Folge der schwierigen wirtschaftlichen Lage war verantwortlich für die Veränderung der Geschlechtsverhältnisse in Kuba, sondern ein resultierendes
administratives Defizit. Darauf sind Scherb et al. in einer weiteren Auswertung auch eingegangen (Scherb et al. 2013). Unabhängig davon bleibt aber allgemein festzustellen, dass bei der Verwendung von aggregierten Daten Vorsicht geboten ist, insbesondere im Hinblick auf Schlussfolgerungen bezüglich komplexer biologischer Effekte. Auf die Schwierigkeiten bei der kausalen Interpretation schwankender Geschlechtsverhältnisse wurde etwa auch im Zusammenhang mit der deutschen Wiedervereinigung hingewiesen, wobei die Schwankungen als zufällig beschrieben wurden (Schnettler und Klüsener 2013).
Es darf und muss angemerkt werden, dass dieses Beispiel nicht beweist, dass die Zeugung/Austragung einer Schwangerschaft in Notzeiten nicht mit einer Veränderung des Geschlechtsverhältnisses der Lebendgeborenen assoziiert ist, sondern nur, dass grob simplifizierende Erklärungsmuster nicht ausreichen.
Grundsätzlich stehen für die Untersuchung von biologischen Phänomenen am Menschen bei Fragen, wie der nach den Determinanten des Geschlechtsverhältnisses der Lebendgeborenen, Erkenntnisse aus adäquaten Tiermodellen sowie aus statistischen bzw. epidemiologischen Beobachtungen zur Verfügung. Ziel der Kapitel 2 und 3 ist es, exemplarisch aufzuzeigen, wie vielfältig das Spektrum potentieller Faktoren ist, die auf den unterschiedlichen Stufen von der Partnerwahl über die Zeugung bis zur Geburt das Geschlechtsverhältnis der Neugeborenen beeinflussen können, und welche Probleme bei der Messung der Zielvariablen „Geschlechtsverhältnis der Lebendgeborenen“ in praxi bestehen. Die wichtigsten Definitionen sind in der Tabelle 1 aufgeführt.
Tab. 1: Definitionen für Schwangerschaftsausgänge und damit zusammenhängende statistische Kennzahlen
| Begriff | Definition |
|---|---|
| Neugeborene | Summe der Lebend- und Totgeburten |
| Lebendgeburt | Mindestens eines von drei Lebensmerkmalen2 |
| Totgeburt | Keines der drei Lebensmerkmale ist aufgetreten, aber das Geburtsgewicht liegt bei mindestens 500 g |
| Fehlgeburt | Eine Geburt, die keines der drei Lebensmerkmale und ein Geburtsgewicht unter 500 g aufweist |
| Frühgeburt | Eine Geburt, die nach einer Schwangerschaftsdauer von weniger als 28 vollendeten Wochen auf die Welt gekommen ist (ICD-10 – P07.2) |
| Säuglingssterblichkeit | Anzahl der Lebendgeborenen, die im ersten Lebensjahr sterben, im Verhältnis zur Gesamtzahl der Lebendgeburten |
| Perinatalsterblichkeit | Summe der Totgeburten und der Lebendgeburten, die in den ersten sieben Lebenstagen versterben, im Verhältnis zur Gesamtzahl der Lebend- und Totgeburten |
| Geschlechtsverhältnis | Verhältnis der Knaben- zu Mädchengeburten |
2 Auswirkungen von Definitionsänderungen auf das Geschlechtsverhältnis von Neugeborenen
2.1 Abgrenzung von Lebend-, Tot- und Fehlgeburten
Neben biologischen Faktoren können auch statistische Klassifizierungen einen Einfluss auf das Geschlechtsverhältnis von Neugeborenen haben, zumindest auf das gemessene. In § 31 der Personenstandsverordnung (BMJ 2011) wird von einer Lebendgeburt gesprochen, „wenn bei einem Neugeborenen nach der Trennung vom Mutterleib entweder das Herz geschlagen oder die Nabelschnur pulsiert oder die natürliche Lungenatmung eingesetzt hat. Hat sich keines der genannten Merkmale des Lebens gezeigt, beträgt das Gewicht der Leibesfrucht jedoch mindestens 500 Gramm, gilt sie als ein tot geborenes Kind. Hat sich keines der Merkmale des Lebens gezeigt und beträgt das Geburtsgewicht weniger als 500 Gramm, handelt es sich um eine Fehlgeburt. Sie wird in den Personenstandsregistern nicht beurkundet“ (BMJ 2011).
Diese Lebendgeburtsdefinition wurde im früheren Bundesgebiet im Jahr 1958 auf Empfehlung der Weltgesundheitsorganisation (WHO) eingeführt und ab 1990 auch in den neuen Bundesländern angewendet. In der DDR waren zuvor von 1957 bis 1990 nicht nur eines sondern zwei Merkmale (Herzschlag und Lungenatmung) für eine Klassifizierung als Lebendgeburt erforderlich. Wenn mehr oder strengere Kriterien im Hinblick auf die Lebensmerkmale oder gar zusätzliche Mindestgrenzen von Geburtsgewicht, Gestationsalter und Körperlänge erfüllt werden müssen, hat dies eine geringere Anzahl registrierter Lebendgeburten zur Folge. Es betrifft vor allem Frühgeborene, die dann unter Umständen statt zu den Lebendgeburten zu den Tot- oder gar Fehlgeburten gerechnet werden.
Die Regelung, wie Tot- und Fehlgeburten voneinander abgegrenzt werden, hat sich zuletzt am 1. April 1994, erneut auf Empfehlung der WHO, geändert und bewirkte eine Senkung des Mindestgeburtsgewichts von Totgeburten von 1 000 Gramm auf 500 Gramm. Das heißt, dass die Fälle mit einem Gewicht von 500 Gramm bis unter 1 000 Gramm seitdem nicht länger zu den Fehl- sondern zu den Totgeburten gezählt werden. Tabelle 2 zeigt die Änderungen im Überblick.
Tab. 2: Definitionsänderungen in Deutschland im Überblick (BiB 2012)
| Kriterien für Lebendgeburt | Kriterien für Totgeburt | ||
|---|---|---|---|
| 1938 bis 1957/1958 | natürliche Lungenatmung | 1938 bis 1979 | mindestens 35 cm lang |
| 1957 bis 1990 (DDR) | Herzschlag und Lungenatmung | 1979 bis 1994 | mindestens 1 000 g schwer |
| seit 1958 (BRD) | ein Lebensmerkmal | seit 1994 | mindestens 500 g schwer |
Im Nachbarland Frankreich (siehe Tabelle 3) gab es in den letzten Jahren ebenfalls mehrere Definitionswechsel. Seit März 1993 gilt dort für Lebendgeburten das Einsetzen der natürlichen Lungenatmung als Kriterium, wie in Deutschland zwischen 1938 und 1957/58. Für die Zeit bis Februar 1993 war von Frankreich wie auch von einigen anderen europäischen Ländern bekannt, dass Lebendgeborene (nach WHO-Definition), die weniger als 24 Stunden überlebt haben, nicht als Lebendgeburten registriert wurden (Masuy-Stroobant 1997). Entscheidend war nicht der Vitalstatus zum Zeitpunkt der Geburt, sondern zum Zeitpunkt der Registrierung, die bis zu 3 Tage oder mehr nach der Geburt erfolgen konnte. Kinder, die lebendig auf die Welt kamen, aber noch vor der Registrierung verstarben, wurden als Totgeburt verzeichnet. Von 1993 bis Ende 2001 galt bei Totgeburten ein Gestationsalter von mindestens 180 Tagen als Kriterium zur Abgrenzung von Fehlgeburten. Häufig fällt dieses Alter bei Totgeborenen jedoch geringer aus. Im November 2001 folgte Frankreich daher auch der WHO-Empfehlung und führte als Kriterium – ähnlich wie in Deutschland seit 1994 – ein Geburtsgewicht von mindestens 500 Gramm oder ersatzweise eine Schwangerschaftsdauer von mindestens 22 Wochen ein. Im August 2008 sind im Rahmen einer weiteren Definitionsänderung diese Kriterien und somit die Abgrenzung zur Fehlgeburt völlig weggefallen (INSEE 2013a, 2013b).
Tab. 3: Definitionsänderungen in Frankreich im Überblick (INSEE 2013a, 2013b)
| Kriterien für Lebendgeburt | Kriterien für Totgeburt | ||
|---|---|---|---|
| bis 1993 | zum Zeitpunkt der Registrierung lebendig | bis 1993 | zum Zeitpunkt der Registrierung tot |
| seit 1993 | natürliche Lungenatmung | 1993 bis 2001 | mindestens 180 Tage |
| 2001 bis 2008 | mindestens 22 Schwangerschaftswochen oder mindestens 500 g schwer | ||
| seit 2008 | keine | ||
2.2 Auswirkungen auf demografische Ziffern
Wie Lebend- und Totgeburten definiert sind, hat nicht nur einen erheblichen Einfluss auf deren gemessene absolute Anzahl, sondern auch auf die mit dieser Anzahl zusammenhängenden demografischen Kennziffern wie die Säuglings- und Perinatalsterblichkeit. Da die Definitionen jedoch von Staat zu Staat verschieden sind, sind internationale Vergleiche dieser Größen ohne Kenntnis der angewandten Definition problematisch. Entsprechendes gilt aufgrund von Definitionsänderungen über längere Zeiträume innerhalb eines Staates.
Für die Berechnung der Säuglingssterblichkeit werden die im ersten Lebensjahr verstorbenen Lebendgeborenen ins Verhältnis zur Gesamtzahl der Lebendgeborenen gesetzt. Die unterschiedlichen Lebendgeburtsdefinitionen in dem Gebiet der DDR (Deutschland-Ost3) und dem früheren Bundesgebiet (Deutschland-West3) waren mit ein Grund dafür, dass die Säuglings- und Perinatalsterblichkeit der DDR zeitweise statistisch unter dem Niveau des früheren Bundesgebietes lag. Abbildung 2 zeigt den verlangsamten Rückgang der Säuglingssterblichkeit im Westen ab 1958 sowie den zeitgleich in der DDR auftretenden deutlichen Rückgang.

Abb. 2: Säuglingssterblichkeit in Deutschland-West und Deutschland-Ost 1946 bis 2012, bezogen auf die Lebendgeborenen des Berichtszeitraums, ab 1958 unter Berücksichtigung der Geburtenentwicklung in den vorangegangenen 12 Monaten (Datenquelle: StBA 2012). Änderung der Definition von Lebendgeburt in der DDR 1957 (1), in der BRD 1958 (2) sowie Übernahme der Definition der BRD in den neuen Bundesländern 1990 (3).
Für die Berechnung der Perinatalsterblichkeit werden Totgeburten und in den ersten sieben Lebenstagen verstorbene Lebendgeburten ins Verhältnis zur Gesamtzahl aller Lebend- und Totgeborenen gesetzt. Hierbei ist nicht die Abgrenzung von Lebend- und Totgeburt entscheidend, sondern die Abgrenzung von Tot- und Fehlgeburt. Durch die letzte Definitionsänderung von Totgeburt im Jahr 1994 stieg nicht nur die absolute Anzahl registrierter Totgeburten, sondern damit auch die Perinatalsterblichkeit (siehe Abbildung 3).
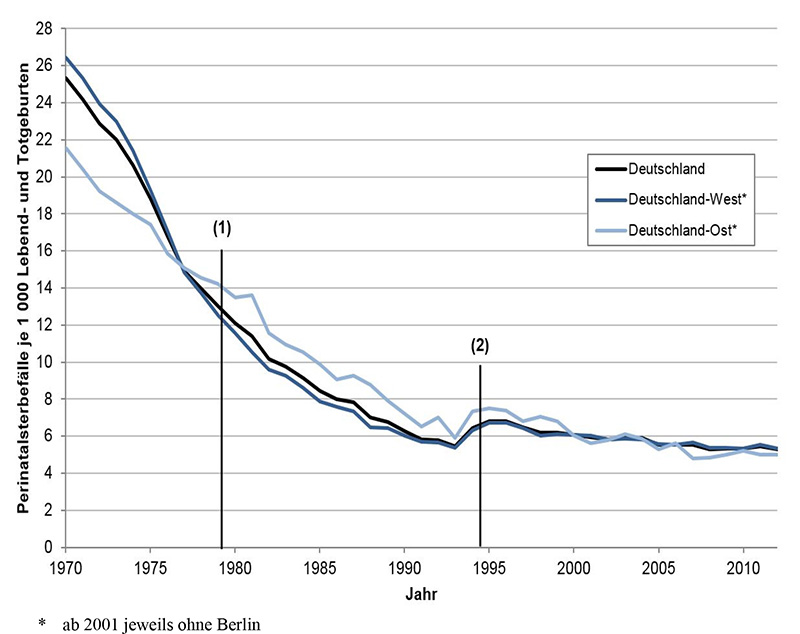
Abb. 3: Perinatalsterblichkeit in Deutschland insgesamt, Deutschland-West und Deutschland-Ost 1970 bis 2010, (Datenquelle: StBA 2012). Änderung der Definition von Totgeburt in der DDR 1979 (1) und der BRD 1994 (2).
Tabelle 4 veranschaulicht die Auswirkungen der Definitionsänderungen in Frankreich auf die Totgeborenenquote4 und die Perinatalsterblichkeit. Im Jahr 2001 waren die französische Totgeborenenquote und Perinatalsterbeziffer schon höher als in vielen anderen EU-Staaten5.
Tab. 4: Totgeborenenquote und Perinatalsterblichkeit in Frankreich (ohne Überseegebiete) ab 2001 (Datenquelle, http://epp.eurostat.ec.europa.eu/portal/page/portal/statistics/search_database)
| 2001 | 2002 | 2003 | 2007 | 2008 | 2009 | |
|---|---|---|---|---|---|---|
| Totgeborenenquote | 4,8 | 8,2 | 8,9 | 9,1 | 10,4 | 11,7 |
| Perinatalsterblichkeit | 6,9 | 10,0 | 10,7 | 10,8 | 12,1 | 13,3 |
Die Definitionsänderung im November 2001 hatte eine drastische Erhöhung der Totgeborenenzahl zur Folge. Durch den Wegfall aller Kriterien im August 2008 erfolgte schließlich ein weiterer Anstieg der Totgeborenenzahl. Gegenwärtig ist die gemessene Perinatalsterblichkeit in Frankreich mehr als doppelt so hoch wie in der Bundesrepublik Deutschland, wo sie bei 5,3 liegt.
2.3 Auswirkungen auf das Geschlechtsverhältnis
Es stellt sich die Frage, inwieweit theoretische Überlegungen, dass die beschriebenen Definitionsänderungen einen Einfluss auf das gemessene Geschlechtsverhältnis bei Geburt haben, durch Zahlen bestätigt werden.
Abbildung 4 zeigt die Entwicklung des Geschlechtsverhältnisses bei Geburt in Deutschland-West und Deutschland-Ost seit 1946 (für die Entwicklung ab 1872 siehe Abbildung 7).
Unter den starken jährlichen Schwankungen fällt in Deutschland-West in erster Linie der Rückgang zwischen 1958 und 1960 auf. Ausgehend vom hohen Nachkriegsniveau beträgt das Geschlechtsverhältnis im Jahr 1957 noch 1,068, im Jahr 1961 hingegen nur noch 1,058. Seitdem pendelt sich das Niveau leicht sinkend bei 1,055 ein. Ob die Definitionsänderung von Lebendgeburt im Jahr 1958 im Zusammenhang mit dem gemessenen Anstieg des Anteils weiblicher Lebendgeborener steht, ist jedoch fraglich. Wenn man davon ausgeht, dass durch eine großzügigere Definition vor allem für Kinder, die die ersten Lebenstage nicht überleben, diese zusätzlich erfasst werden, wäre es unplausibel, dass hierdurch in den späten 1950er Jahren vor allem weibliche Geburten betroffen sein sollten. Da zudem in der Entwicklung des Geschlechtsverhältnisses der Totgeborenen (Abbildung 5) keine entgegengesetzte Niveauverschiebung zum gleichen Zeitpunkt einsetzt, ist nicht davon auszugehen, dass die Definitionsänderung von 1958 eine Veränderung des Geschlechtsverhältnisses der Lebendgeburten bewirkt hat.
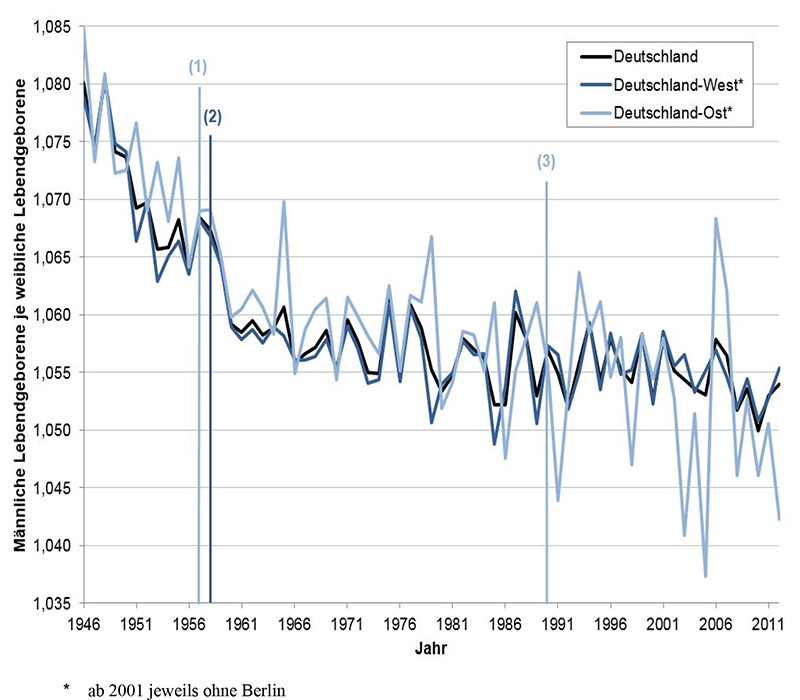
Abb. 4: Geschlechtsverhältnis der Lebendgeborenen in Deutschland-West und Deutschland-Ost sowie in Deutschland insgesamt, 1946 bis 2012 (Datenquelle: StBA 2012). Änderung der Definition von Lebendgeburt in der DDR 1957 (1), in der BRD 1958 (2) sowie Übernahme der Definition der BRD in den neuen Bundesländern 1990 (3).
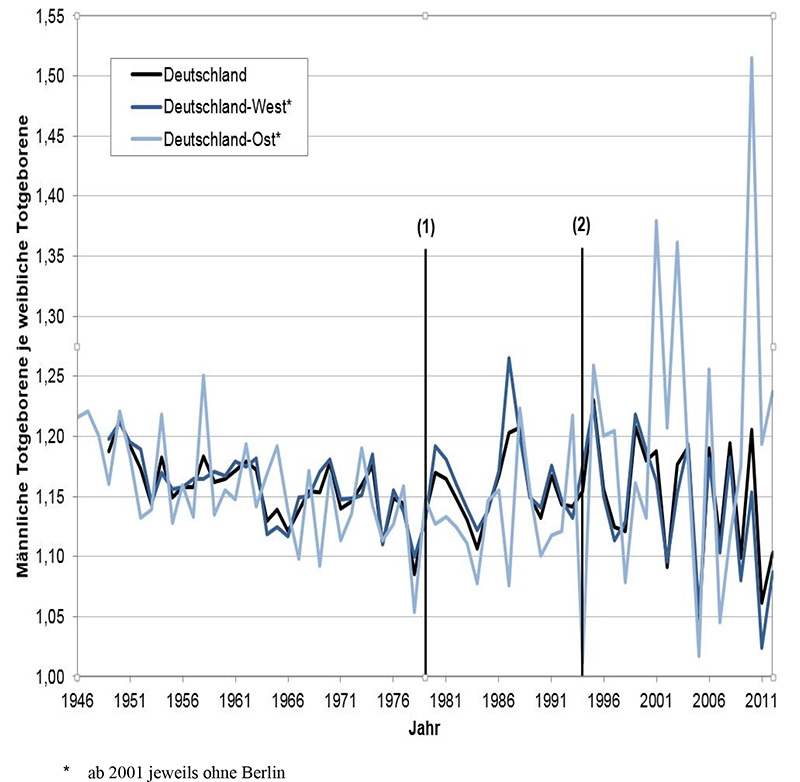
Abb. 5: Geschlechtsverhältnis der Totgeborenen in Deutschland-West und Deutschland-Ost sowie in Deutschland insgesamt, 1946 bis 2012 (Datenquelle: StBA 2012). Änderung der Definition von Totgeburt in der DDR 1979 (1) und der BRD 1994 (2).
In der DDR erfolgte im Jahr 1957 ebenfalls eine Definitionsänderung. Auch hier zeigt sich zwar ein Rückgang zwischen 1958 und 1960 (von 1,069 auf 1,060). Während jedoch die Definitionsänderung in der BRD einen Anstieg der Anzahl der Lebendgeborenen bei gleichzeitigem Rückgang der Anzahl der Totgeburten bewirkt haben muss, hätte der gegenteilige Effekt durch die Änderung in der DDR eintreten müssen. Dass aber in beiden Teilen Deutschlands ein Rückgang des Geschlechtsverhältnisses einsetzte (siehe Abbildung 7), hängt wohl in erster Linie damit zusammen, dass sich das Geschlechtsverhältnis nach dem Krieg wieder normalisierte und sich schließlich auf ein Niveau einpendelte, das – wie schon vor dem ersten Weltkrieg – zwischen 1,05 und 1,06 liegt (StBA 2012). Auch die Einführung der Definition der BRD 1990/1991 führt zu einer Reduktion, jedoch folgt im Jahr 1992 ein umso größerer Anstieg. Eine definitionsbedingte Niveauverschiebung ist nicht erkennbar. Die Abbildung 5 zeigt auch den deutlichen Einfluss des Rückgangs der absoluten Zahl an Totgeburten auf die Varianz des Geschlechtsverhältnisses, die im Laufe der Jahre deutlich zunimmt und in den neuen Bundesländern aufgrund kleinerer Fallzahlen besonders hoch ist.
Dass im Zuge der Definitionsänderung für Totgeburten ab 1994 eine systematische Veränderung des Geschlechtsverhältnisses einsetzte, kann in Abbildung 5 nicht bestätigt werden. Auch die Definitionsänderung von 1979 lässt keine Niveauverschiebung erkennbar werden. Die Werte schwanken im ganzen Zeitraum überwiegend – recht konstant – zwischen 1,1 und 1,2.
Da sich das Geschlechtsverhältnis bei Totgeburten auf einem höheren Niveau befindet als bei Lebendgeborenen, wäre ein Anstieg des Geschlechtsverhältnisses durch eine Definitionsänderung, die zuvor als totgeboren Klassifizierte als Lebendgeburt einordnet, nachvollziehbar gewesen. Dieser Effekt ist in den deutschen Daten allerdings nicht beobachtbar.
Veränderungen des Geschlechtsverhältnisses bei Geburt durch Definitionsänderungen sind für Deutschland daher nicht belegbar.
In Frankreich (siehe Abbildung 6) schwankte das Geschlechtsverhältnis der Lebendgeborenen in den vergangenen 60 Jahren zwischen 1,04 und 1,06 und pendelt sich seit 10 Jahren zunehmend auf einen Wert unterhalb von 1,05 ein. Ab dem Jahr 1993, in dem der letzte Definitionswechsel von Lebendgeburt durchgeführt wurde, ist für das Geschlechtsverhältnis der Lebendgeborenen ein Rückgang, für jenes der Totgeborenen ein Anstieg zu verzeichnen. Weiterhin ist auffällig, dass die Kurve des Geschlechtsverhältnisses der Totgeborenen nicht annähernd so konstant verläuft wie in Deutschland. Es ist auffällig, dass gerade in den 1970er und 1980er Jahren, in denen der Wert für die Totgeburten besonders niedrig ist, der Wert für Lebendgeburten vergleichsweise hoch ist, und umgekehrt für die 1950er und 1960er Jahre sowie die letzten Jahre ab 2008. Ein definitorischer Zusammenhang, vielleicht eine Definitionsänderung um das Jahr 1970, wäre als Erklärung naheliegend, laut Auskunft des französischen Instituts für Statistik und Ökonomische Studien (INSEE) gab es jedoch keine definitorischen Anpassungen zwischen 1946 und 1993.
Dass sich Definitionsänderungen stärker auf die Anzahl der Totgeburten auswirken können als auf jene der Lebendgeburten hängt mit der wesentlich niedrigeren Anzahl von Totgeburten zusammen. Ab 1993 lässt sich ein kurzzeitiges Hoch des Geschlechtsverhältnisses in der Kurve der Totgeburten feststellen, während im gleichen Zeitraum das Niveau bei den Lebendgeburten vergleichsweise gering ist. Für die Jahre 2000 bis 2002 waren keine Daten zum Geschlecht der Totgeborenen verfügbar, jedoch insbesondere ab 2008, nach dem Wegfall der Abgrenzung zur Fehlgeburt, kann man beobachten, dass das Verhältnis bei Totgeburten deutlich nach oben geht. Allgemein kann man sagen, dass je mehr frühe und untergewichtige Geburten in die Auswahlgesamtheit einbezogen werden, desto höher ist wahrscheinlich das Geschlechtsverhältnis. Dies wird am Beispiel Frankreichs deutlicher als am Beispiel Deutschlands.
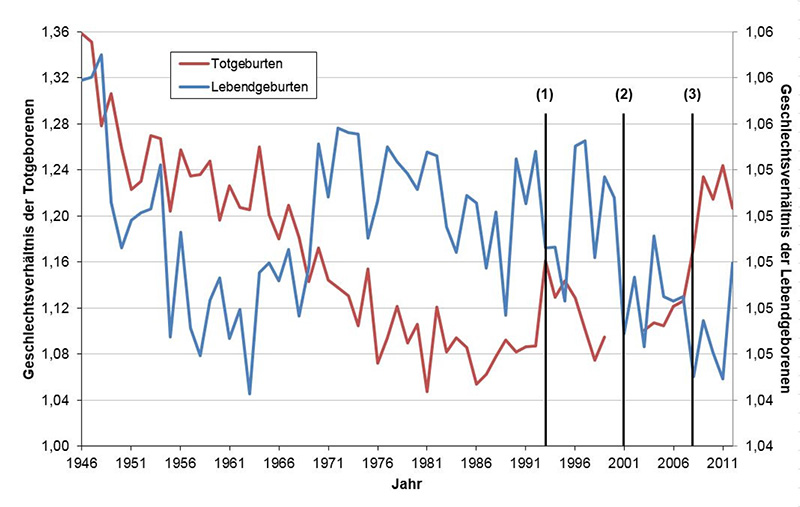
Abb. 6: Geschlechtsverhältnis der Lebend- und Totgeborenen in Frankreich (ohne Überseegebiete), 1946 bis 2012. Änderung der Definition von Lebend- und Totgeburt 1993 (1) sowie von Totgeburt 2001 (2) und 2008 (3). (Datenquelle: Institut national de la statistique et des études économiques; statistiques de l’état civil, INSEE)
3 Beispiele aus der Epidemiologie
Zur Interpretation der Zahlenwerte des Geschlechtsverhältnisses ist Folgendes zu beachten:
Ein Geschlechtsverhältnis von z. B. 1,05 bedeutet, dass auf 100 lebendgeborene Mädchen 105 Jungen registriert wurden. Das würde einen Anteil von 51,2 % Jungen bedeuten. Damit entspricht eine Änderung des Verhältnisses um ca. 0,01 (z. B. von 1,06 auf 1,05 entsprechend 51,5 % auf 51,2 %) einer Änderung von 0,3 Prozentpunkten6.
Um eine derartige Veränderung (von 1,06 auf 1,05) unter der Annahme einer Binomialverteilung statistisch absichern zu können (β=0,9 oder β=0,8; α=0,05) würde man 937 105 oder 700 215, also je nach Power rund 0,7 bis 1 Million Geburten pro Vergleichsgruppe beobachten müssen. Die Zahl der Lebendgeborenen in der Bundesrepublik Deutschland lag 2011 bei 662 712, im Jahre 1991 bei 830 019.
Jedoch wurde beobachtet, dass die Streuung der jährlichen Schwankungen größer ist, als man auf Basis einer Binomialverteilung erwarten kann. Die Ursache hierfür muss in der Zusammensetzung der betrachteten Bevölkerung aus Untergruppen mit jeweils unterschiedlichem Basis-Geschlechtsverhältnis liegen; welche Gruppen dies sein könnten, ist für die Bundesrepublik Deutschland nicht bekannt. In den USA zeigen sich Anzeichen hierfür in Form der ethnischen Untergruppen (Mathews und Hamilton 2005). Dies bewirkt, dass die Absicherung von zeitlichen Veränderungen noch größere Bevölkerungszahlen als die oben genannten erfordert. Zeitliche Änderungen können auch durch Verschiebungen innerhalb der unbekannten Untergruppen bzw. bezüglich deren Anteilen zustande kommen.
Diese zusätzliche Streuung wird in statistischen Modellen als Überdispersion7 bezeichnet und ihre Größe kann mit Hilfe eines sogenannten Skalenparameters geschätzt werden. Auf diese Weise kann man das Phänomen beschreiben, jedoch nicht erklären.
Die Beobachtung von Änderungen in dieser Größenordnung in kleinen Regionen oder Gruppen ist damit im Allgemeinen nicht vom Zufall unterscheidbar.
3.1 Trends des Geschlechtsverhältnisses
Die Arbeit von Catalano (2003) sowie die durch das Statistische Bundesamt (wwww.destatis.de) veröffentlichten Daten zeigen eine Zeitreihe des Geschlechtsverhältnisses in Deutschland-West und Deutschland-Ost ab 1946 (siehe Abbildung 7). Sie zeigen eine eindeutige Abnahme von Werten um 1,08 auf Werte im Bereich von 1,05 bis 1,06 von 1946 bis 1960, und relativ konstante Werte mit einem schwachen Abwärtstrend ab 1960. Die Zeitreihe ab 1946 relativiert sich, wenn man Zahlen für Deutschland8 ab 1870 hinzuzieht. Im Vergleich zu den deutlichen Anstiegen des Geschlechtsverhältnisses in und nach den beiden Weltkriegen (Bromen und Jöckel 1997a; van den Broek 1997) sind die Schwankungen seit 1960 vernachlässigbar. Jedoch auch in den Kriegszeiten war der Anteil der Jungen allerhöchstens 0,519 (Geschlechtsverhältnis 1,08) gegenüber 0,514 (Geschlechtsverhältnis 1,056) seit 1960, dies ist ein Unterschied von 0,5 Prozentpunkten.
Bis 1960 zeigt sich in den USA nach dem Krieg eine erhebliche Abnahme des Anteils der Jungen (Mathews und Hamilton 2005), dem jedoch bis 1970 ein leichter Anstieg folgt, bevor wieder der auch sonst in den entwickelten Ländern beobachtete (Davis et al. 1998) leichte Abwärtstrend um insgesamt ca. 0,2 Prozentpunkte seit 1960 oder 1970 einsetzt.
Catalano und Bruckner (2005) beschreiben für Schweden im Zeitraum 1862 bis 1991 eine generelle positive Assoziation zwischen einem Maß für Wohlstand und dem Anteil an Jungen. Das Geschlechtsverhältnis schwankte im gesamten Zeitraum etwa von 1,045 bis 1,07, mit besonders hohen Werten in den 1950er Jahren, wie es auch in Deutschland beobachtet wurde. Allerdings war dem in Schweden nicht der in Deutschland beobachtete erhebliche Anstieg im Geschlechtsverhältnis im Zusammenhang mit den Weltkriegen vorausgegangen.
Im Gegensatz dazu berichten Catalano et al. weiterhin über in den USA und Schweden als Stressreaktion reduzierte Jungenanteile (Catalano et al. 2005, Catalano et al. 2006). Die Studie von Catalano et al. (2006) zu den Auswirkungen des Anschlages vom 11. September 2001 auf das Geschlechtsverhältnis der später geborenen Kinder in New York City zeigte zwar einen Effekt in Richtung weniger Jungen, der allerdings nur für einen Monat signifikant war (Januar 2002), also etwa 3 bis 4 Monate nach den Anschlägen. Die von den Autoren angeführte Begründung für die somit notwendig höhere Abortrate von männlichen Föten in der ca. 20. bis 24. Schwangerschaftswoche ist sehr spekulativ, und die Fallzahlen sind vergleichsweise gering, so dass dieser Studie kein großes Gewicht beizumessen ist.
Ein Review von Fellman und Eriksson (2011) konnte für die skandinavischen Länder keine gesicherten Erkenntnisse bezüglich der Ursachen der beobachteten Schwankungen des Geschlechtsverhältnisses ausmachen. Sie beobachteten, ähnlich wie in den anderen Arbeiten und Ländern, Anstiege bis 1950 und ein erhebliches Absinken seither. Als Gesamteindruck ergibt sich aus diesen Arbeiten: Extreme Notzeiten und Stressereignisse und die darauf folgenden Jahre stellen erhebliche Ausnahmesituationen in Bezug auf das Geschlechtsverhältnis dar, deren Richtung jedoch offenbar unterschiedlich sein kann. In westlichen Ländern sinkt seit der Nachkriegszeit der Jungenanteil langsam, aber kontinuierlich.
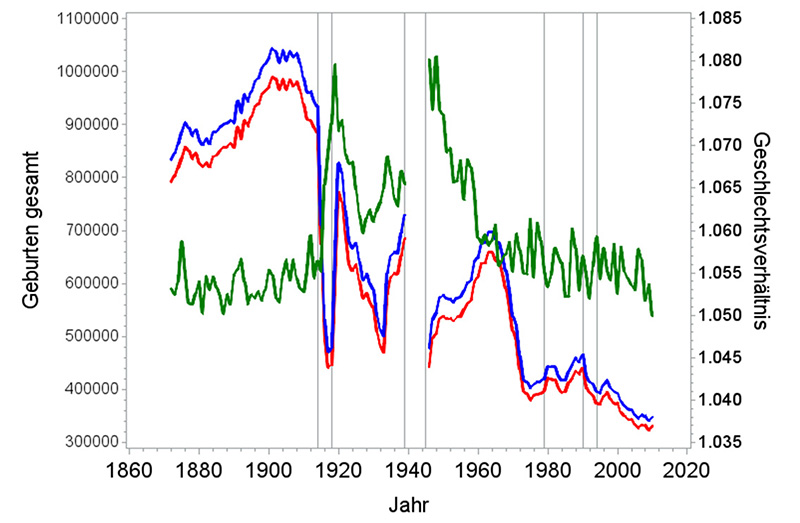
Abb. 7: Verlauf der Geburtenzahl (blau: männlich, rot: weiblich) in Deutschland9 von 1872 bis 2010 sowie des sich daraus ergebenden Geschlechtsverhältnisses (grün). Für den Zeitraum des zweiten Weltkriegs liegen keine Daten vor (Datenquelle: StBA 1972, 2012). Die senkrechten Linien zeigen Anfang und Ende der Weltkriege sowie die Jahre der Definitionsänderungen der Lebendgeburten.
3.2 Ländervergleiche
Zu ausdrücklichen Ländervergleichen wurde nur eine Literaturstelle gefunden. Barber (2004) untersucht ökologisch nach Ländern den Einfluss von Polygamie, allgemeiner Fertilität bzw. Geburtsreihenfolge, Alter der Mutter und Kontrazeption. Monogamie, jüngere Mütter, niedrigere Fertilität (weniger Kinder pro Familie), Erstgeburten und verbreitete Kontrazeption führen allgemein zu mehr Jungen. Dabei sind die oben genannten Faktoren nicht unabhängig. Barber interpretiert, dass Faktoren, die zu häufigerem Geschlechtsverkehr führen (Monogamie, jüngere Personen, jung Verheiratete), die Geburt eines Jungen begünstigen.
3.3 Alter der Eltern und Geburtsreihenfolge
Diese Themen müssen gemeinsam betrachtet werden, da sie auf Bevölkerungsebene miteinander korreliert sind.
Jacobsen et al. (1999) finden in Dänemark keine Beziehung des Geschlechtsverhältnisses zum Alter der Mutter und zur Geburtsordnung. Davis et al. (1998) zitieren in ihrer Übersichtsarbeit zwei Arbeiten, die eine Abnahme der Anzahl an Jungen mit dem zunehmenden Alter der Eltern in Beziehung setzen. In den USA ist die Entwicklung des Geschlechtsverhältnisses und des Alters der Mütter (siehe unten) unterschiedlich nach Bevölkerungsgruppen, deren Anteile sich auch im Laufe der Jahre verschieben. Damit sind die Gesamtzahlen auch mit Vorsicht zu interpretieren. Mathews und Hamilton (2005) sehen in den USA auch eine deutliche Zunahme des Mädchenanteils mit höherem Alter der Mutter sowie mit der Geburtsreihenfolge. Biggar et al. (1999) sehen für Dänemark eine Abhängigkeit von der Familiengröße mit höherem Mädchenanteil in kleineren Familien, was der Beobachtung in den USA teilweise widerspricht. Es gibt zumindest eine zeitliche Assoziation zwischen der in Dänemark seit den 1950er Jahren gesunkenen Familiengröße und dem zunehmenden Anteil von Mädchen. Die Veränderung bewegt sich in einer Größenordnung von unter 0,3 Prozentpunkten. Es muss aber als unplausibel angesehen werden, dass dieses Phänomen geeignet ist, auf einer globalen Ebene über einen langen Zeitraum die Schwankungen des Geschlechtsverhältnisses zu erklären (Jöckel und Bromen 2000).
3.4 Assistierte Reproduktion
Luke et al. (2009) erwähnen in Bezug auf Einlingsgeburten, dass die intrazytoplasmatische Spermieninjektion (ICSI) eher das Geschlechtsverhältnis senkt. Assistierte Reproduktion kann laut Dean et al. (2010) das Geschlechtsverhältnis beeinflussen, dabei hängt die Richtung jedoch von dem gewählten Vorgehen ab, außerdem haben sich die Prozeduren seit deren Einführung drastisch verändert. Der mittlere beobachtete Jungenanteil schwankte in der Studie je nach Vorgehen zwischen 56 % und 49 %. Insgesamt war der Jungenanteil nach assistierter Reproduktion in dieser Studie 51,3 %, was sich nicht signifikant von der australischen Vergleichspopulation (Jungenanteil 51,5 %) unterscheidet. Aufgrund der betrachteten kleinen Fallzahlen in den genannten Arbeiten müsste ein Effekt jedoch schon sehr erheblich sein, um relevant und signifikant zu sein.
3.5 Frühgeburten und Totgeburten
Die Zahl und der Anteil der Totgeburten hat seit dem Ende des 2. Weltkrieges gleichmäßig abgenommen, unabhängig von der Gesamtzahl der Geburten, dies kann als Indikator für den medizinischen Fortschritt gewertet werden (siehe auch Kapitel 2). Bromen und Jöckel (1997b) haben gezeigt, dass die Entwicklung bei den Totgeburten aufgrund eines weitgehend stabilen Anteils an Jungen unter den Totgeburten die Gesamtentwicklung wohl nicht beeinflusst, Ähnliches berichten Biggar et al. (1999) für Dänemark. Jedoch geht aus den amtlichen Daten hervor und wurde wiederholt beschrieben (van den Broek 1997), dass ein größerer Anteil der Totgeburten Jungen sind. Das Geschlechtsverhältnis bei den Totgeburten beträgt in Deutschland seit 1948 relativ konstant 1,16 (StBA 2012); aufgrund der kleinen Fallzahlen sind die jährlichen Zufallsschwankungen jedoch sehr groß. Bei dem beobachteten sinkenden Anteil der Totgeburten müsste dies, wenn es in nennenswertem Umfang das Geschlechtsverhältnis der Lebendgeborenen beeinflussen würde, entsprechend tendenziell zu einem Anstieg des Geschlechtsverhältnisses führen, es wird jedoch ein Absinken beobachtet.
Hassold et al. (1983) berichten ein höheres Geschlechtsverhältnis (1,3) bei Spontanaborten; inwieweit dies das Geschlechtsverhältnis bei Frühgeburten beeinflusst, ist jedoch unklar.
In einer Dissertation aus Rostock aus dem Jahr 2008 wurden Geschlechtsverhältnisse von je nach Zeitraum 1,017 bis 1,054 nach normaler Schwangerschaftsdauer und von 1,103 bis 1,195 für Frühgeburten angegeben (Nierling 2008). Sehr frühe Frühgeburten wurden deutlich häufiger bei Jungen beobachtet. Der ebenfalls beschriebene steigende Anteil von Frühgeburten an den Geburten insgesamt müsste analog zu den Überlegungen in Bezug auf die Totgeburten bei einem kausalen Zusammenhang zu einer Erhöhung des Jungenanteils führen, tendenziell wurde jedoch eher eine Abnahme über alle Geburten beobachtet. Die Beobachtungen beziehen sich auf die Jahre 2000 bis 2006 und insgesamt ca. 15 000 Geburten mit 8 % bis 10 % Frühgeburten, was in Bezug auf das Geschlechtsverhältnis eine Datenlage mit geringer Power bedeutet.
3.6 Zeitreihenbetrachtungen in Deutschland seit 1946
Im Folgenden soll gezeigt werden, dass Auswertungen relativ kurzer Zeitreihen je nach vorgegebenen Modellannahmen zu eher willkürlichen Ergebnissen führen müssen. Daten zum Geschlechtsverhältnis müssen als binomialverteilt mit Überdispersion betrachtet werden. Daher empfiehlt sich ein generalisiertes lineares Modell (Verteilungsannahme = binomial, link = logit und gleichzeitiger Schätzung eines Skalenparameters). Abhängige Variable ist die Anzahl der Jungen bezogen auf die Gesamtzahl der Geburten.
Etwas willkürlich wurde zu Demonstrationszwecken der Zeitraum 1973 bis 2009 ausgewählt. Der Datensatz hat 37 Datenpunkte. Der Skalierungsfaktor der verwendeten Daten beträgt 1,09, also weisen die Daten 9 % mehr Varianz auf als zu erwarten wäre.
In der folgenden Abbildung 8 sind die jeweiligen punktweisen 95 %-Konfidenzbereiche um das Gesamtmittel entsprechend der jeweiligen Gesamtzahl aufgetragen, jeweils mit und ohne Skalierungsfaktor. Zu erwarten sind zufällig ca. 2 Punkte außerhalb dieses Bereichs, dies wird in etwa auch so beobachtet.
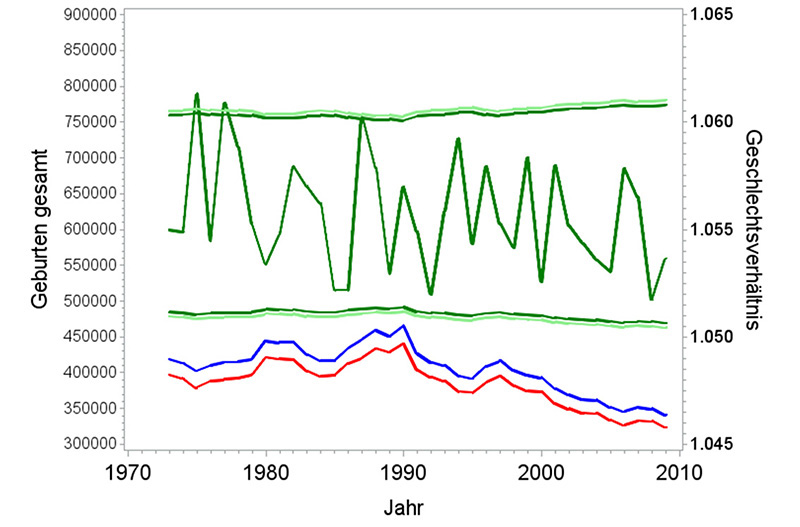
Abb. 8: Verlauf der Geburtenzahl (blau: männlich, rot: weiblich) in Deutschland insgesamt von 1973 bis 2009 sowie des sich daraus ergebenden Geschlechtsverhältnisses (grün). Die Linien oberhalb und unterhalb geben den Bereich an, in dem sich 95 % der Werte bewegen müssten, grün: unter dem Binomialmodell, hellgrün: unter Berücksichtigung der Überdispersion (Datenquelle: StBA 2012).
Die relativ wenigen vorliegenden Ausprägungen sowie die im Verhältnis zur Wertgröße erhebliche Schwankungsbreite führen zu der Problematik, dass die gewählte Vorgehensweise bei der Anpassung einer Regressionslinie die Ergebnisse erheblich beeinflussen kann.
Im Folgenden sollen drei Varianten kurz exemplarisch vorgestellt werden:
- –
-
Knickpunktanalyse (Join points),
- –
-
Sprungpunktanalyse (Jump points) und
- –
-
eine Kombination beider.
Bei der ersten Variante sind nur Änderungen des Trends (Knicke) zulässig. Bei der zweiten Vorgehensweise wird ein konstanter Trend angenommen, jedoch sind plötzliche Änderungen des Basis-Geschlechtsverhältnisses (Sprungpunkte) erlaubt. Bei der dritten Variante kann sich an Sprungpunkten auch die Steigung der Kurve verändern. Wie viele und an welchen Stellen ein Sprung und/oder Knick vorliegt, wird anhand der Modellanpassung entschieden. Die folgenden drei Modelle sind unter den gemachten Einschränkungen jeweils „optimal“, d. h. unter dem gewählten Optimalitätskriterium des Akaike Information Criterion (AIC) lässt sich durch einen weiteren Sprung oder Knick keine weitere Verbesserung erzielen. Diese Vorgehensweise ist rein deskriptiv und nicht hypothesengesteuert. Daher machen in diesem Zusammenhang Signifikanzaussagen auch keinen Sinn.
Insbesondere bei der Betrachtung sehr kurzer Zeiträume wird das gefundene Zeitmuster immer zufälliger, hier demonstriert am Beispiel der Zeitreihen ab 1973.
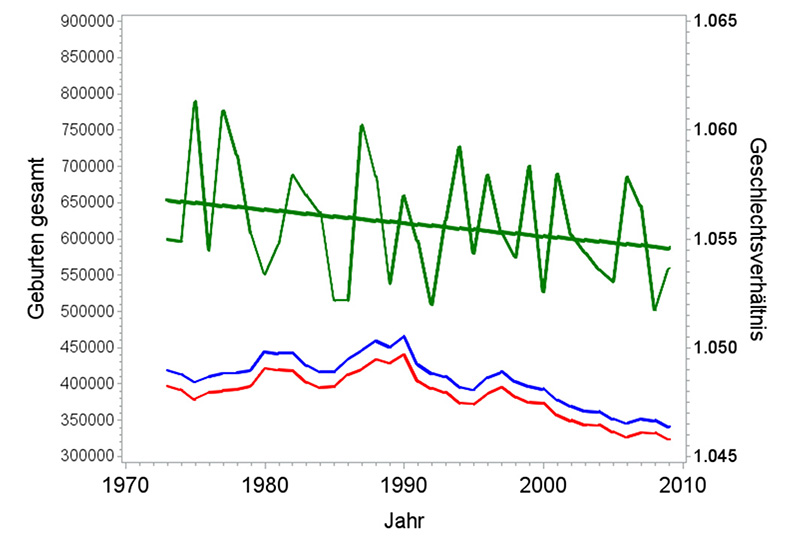
Abb. 9: Knickpunktmodell: Verlauf der Geburtenzahl (blau: männlich, rot: weiblich) in Deutschland insgesamt von 1973 bis 2010 sowie des sich daraus ergebenden Geschlechtsverhältnisses (grün, beobachtetes und angepasstes Geschlechtsverhältnis) (Datenquelle: StBA 2012).
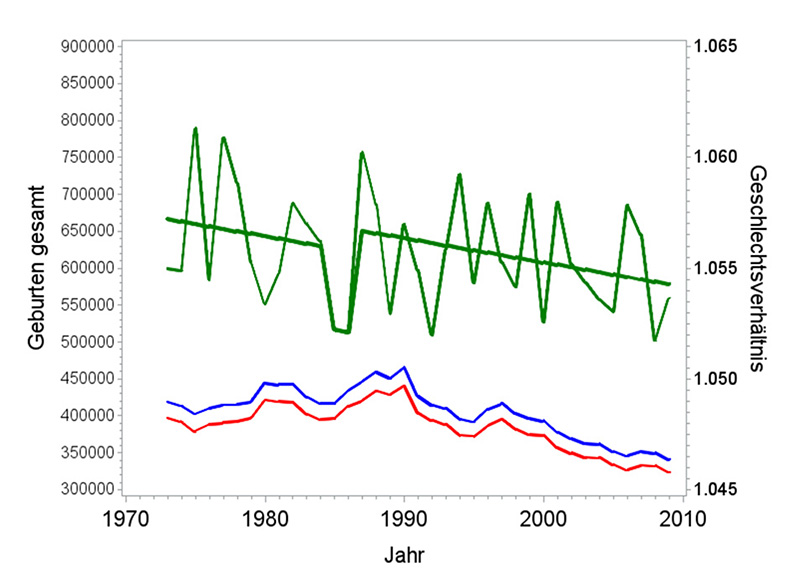
Abb. 10: Sprungpunktmodell: Verlauf der Geburtenzahl (blau: männlich, rot: weiblich) in Deutschland insgesamt von 1973 bis 2010 sowie des sich daraus ergebenden Geschlechtsverhältnisses (grün, beobachtetes und angepasstes Geschlechtsverhältnis) (Datenquelle: StBA 2012).
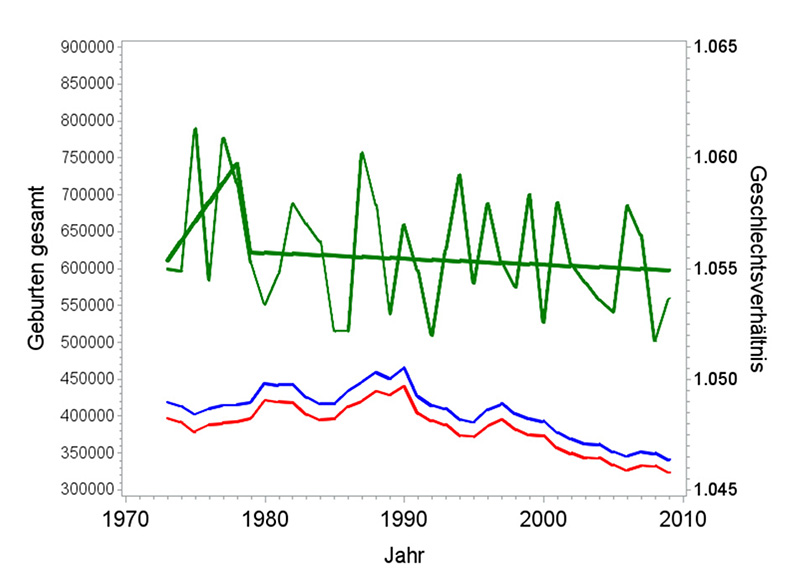
Abb. 11: Kombiniertes Modell: Verlauf der Geburtenzahl (blau: männlich, rot: weiblich) in Deutschland insgesamt von 1973 bis 2010 sowie des sich daraus ergebenden Geschlechtsverhältnisses (grün, beobachtetes und angepasstes Geschlechtsverhältnis) (Datenquelle: StBA 2012).
Die drei Modellvorgaben führen zu völlig unterschiedlichen Schlussfolgerungen. Das erste Modell fand keinen Knick. Das nächste fand zwei Sprungpunkte, die die Jahre 1985 und 1986 als ungewöhnlich niedrig (mehr Mädchen) herausgriffen, wobei der optische Eindruck zeigt, dass zwei aufeinanderfolgende Jahre mit eher niedrigen Werten ebenfalls vorkommen können, ohne dass das etwas zu bedeuten hat. Das dritte Modell schließlich beschreibt ziemlich unsinnig einen steilen Anstieg in den ersten sechs Jahren, der keinesfalls so weitergehen kann. Insbesondere an den Rändern solcher Datensätze ändern sich die Schussfolgerungen möglicherweise drastisch, wenn man ein weiteres Jahr hinzunimmt oder weglässt.
Zusammengefasst ist festzustellen: In Zeitreihen dieser Art von 40 bis 50 Jahren kann man je nach beschreibendem Modell mit Hilfe explorativer Analysen so ziemlich alles hineininterpretieren oder „herausholen“, was man möchte. Die sehr hohen absoluten Geburtenzahlen in Deutschland insgesamt lassen dabei auch fast jeden kleinen Knick oder Sprung „signifikant“ erscheinen. Hier wurde sich auf drei denkbare Modelle beschränkt, sehr viel mehr sind möglich. Wird eine derartige Modellanpassung in der Literatur vorgestellt, so bleibt auch immer die Frage, wie viele weitere noch berechnet wurden und auf welcher Basis eine zur Präsentation ausgewählt wurde.
4 Studien zu ionisierender Strahlung
4.1 Atombombenüberlebende von Hiroshima und Nagasaki
Das Geschlechtsverhältnis bei den Nachkommen von Atombombenüberlebenden wurde in mehreren Publikationen, an denen W. J. Schull und J. V. Neel maßgeblich beteiligt waren, untersucht.
In einer ersten Analyse (Schull und Neel 1958) wurden Informationen zu den Geburtsjahrgängen 1948 bis 1955 erfasst. Bis 1953 wurden diese Informationen über Ärzte gewonnen, für die Jahrgänge 1954 und 1955 über Geburtsregister und Fragebögen, die sich an die Eltern richteten. Aufgrund der kulturellen Gepflogenheit in Japan, dass auch Verwandte heiraten konnten (s. Schull 1958), wurde für den Zeitraum 1948 bis 1953 noch einmal eine Unterteilung nach Kindern verwandter und nicht verwandter Eltern vorgenommen. Hinsichtlich der Strahlenexposition wurden drei Gruppen gebildet: nur die Mutter exponiert; nur der Vater exponiert; beide exponiert. In jeder Gruppe gab es mehrere Expositionskategorien, mindestens aber drei, wobei die Dosis in reps angegeben wurde (roentgen equivalent physical; 1 rep ist etwas mehr als 0,01 Gy). Es ergaben sich insgesamt 12 Gruppen, für die eine Regressionsanalyse durchgeführt wurde. Die Analysen konnten auf der Basis von 139 084 Geburten aus den Städten Hiroshima und Nagasaki durchgeführt werden. In elf der zwölf Analysen ergaben sich Regressionskoeffizienten, die die Autoren auf Grund biologischer Überlegungen erwartet hatten: ein Anstieg des Anteils geborener Knaben, wenn der Vater exponiert war, und ein Anstieg des Anteils geborener Mädchen, wenn die Mutter exponiert war. Dies galt jeweils unabhängig vom Expositionsstatus des anderen Elternteils. Einer der Koeffizienten (Jahrgänge 1948 bis 1953, nicht verwandte Eltern, nur die Mutter war exponiert) erreichte dabei statistische Signifikanz. Eine Analyse, die die Exposition beider Elternteile gleichzeitig berücksichtigt, wurde nicht durchgeführt.
In einer späteren Analyse (Schull et al. 1966) wurden zusätzlich die Geburtsjahrgänge 1956 bis 1962 eingeschlossen, wodurch die Zahl der Geburten um weitere 47 624 auf 186 708 erhöht werden konnte. In die Analyse gingen dabei 140 524 Geburten ein, für die ausreichende Information vorlag (leider fehlt eine entsprechende Information für die Publikation von 1958). Die in der Publikation von 1958 beschriebenen Ergebnisse zeigten sich jetzt nicht mehr. Die Regressionskoeffizienten bezüglich des Geschlechtsverhältnisses wiesen nicht mehr die deutliche Tendenz auf, die sich in der vorherigen Analyse gezeigt hatte. Die Autoren stellen fest, dass es unter Hinzunahme der neuen Daten nunmehr sechzehn Regressionskoeffizienten statt der früheren zwölf gibt, und dass davon nur einer (verwandte Eltern, nur die Mutter exponiert, Geburtsjahrgangszeitraum 1948 bis 1953) signifikant verschieden von Null ist. Die Prüfung der Regressionskoeffizienten bezüglich Richtung und Ausmaß der Veränderungen zeigten nicht mehr das vorherige eindeutige Muster. Die Verteilung der Vorzeichen der Regressionskoeffizienten (sechs von acht im Zusammenhang mit väterlicher Exposition sind positiv, drei von acht im Zusammenhang mit mütterlicher Exposition sind positiv) widersprach nicht der Nullhypothese, nämlich dass die Strahlenexposition keinen Einfluss auf das Geschlechtsverhältnis hat bzw. dass die Vorzeichen dementsprechend in etwa gleich häufig positiv oder negativ sein müssten. Werden die Daten nicht in den verschiedenen Kategorien analysiert, sondern zusammengefasst, so zeigt sich kein signifikanter Zusammenhang zwischen der Strahlenexposition der Eltern und dem Geschlechtsverhältnis, weder bei mütterlicher noch bei väterlicher Exposition. Hinzu kommt, dass insbesondere für Hiroshima zum Zeitpunkt der Publikation die Dosisabschätzungen revidiert wurden, was hinsichtlich der Analyse des Geschlechtsverhältnisses dazu führte, dass die Regressionskoeffizienten, wie sie in der Arbeit aufgeführt wurden, als zu hoch bezeichnet werden mussten (Schull et al. 196610). Abschließend konstatieren die Autoren, dass der ursprüngliche Befund eines Einflusses der Strahlenexposition der Eltern auf das Geschlechtsverhältnis durch die neue Analyse nicht bestätigt wurde. Wenn überhaupt zeigte sich ein Effekt hin zu einem höheren Anteil von Mädchen. Die Autoren konstatieren vorsichtig, dass es möglicherweise einen kleinen frühen Effekt hin zu einem kleineren Anteil von Mädchen gab, der mit zunehmender Beobachtungsdauer verschwunden ist. Es kann aber auch sein, dass der ursprüngliche Befund keine biologische Bedeutung hat. Nach 1958 gewonnene Erkenntnisse der Biologie hatten dazu geführt, dass sich die Sichtweise der Autoren hinsichtlich der möglichen genetischen Auswirkungen einer Strahlenexposition änderte (Neel 1963) und sie jetzt das Geschlechtsverhältnis nicht mehr für eine sinnvolle Zielvariable hielten: „We have repeatedly stressed the unsatisfactory nature of the sex ratio as a variable“.
In einer weiteren Analyse (Neel et al. 1990), in der acht verschiedene Parameter bei den Nachkommen von Atombombenüberlebenden hinsichtlich möglicher genetischer Effekte untersucht wurden, verzichteten die Autoren trotz der in der Zwischenzeit erneut revidierten Dosimetrie (DS86 statt T65DR) auf eine erneute Analyse des Geschlechtsverhältnisses. Sie begründeten dies damit, dass die vorherige Analyse aus dem Jahre 1966 eher in die Richtung auf eine Verschiebung hin zu einem größeren Anteil von Mädchen hindeutete – wenngleich statistisch nicht signifikant – und damit nicht die Hypothese einer Veränderung des Geschlechtsverhältnisses hin zu einem größeren Anteil von Jungen unterstützte.
Eine Auswertung auf der Basis des DS86 und eines nochmals erweiterten Datensatzes, der die Geburtsjahrgänge bis 1984 einschloss, kam zu dem gleichen Ergebnis wie die Auswertung von 1990, nämlich ein nicht signifikanter Effekt hin zu einem größeren Anteil von Mädchen (Yoshimoto et al. 1991).
4.2 Beschäftigte in britischen kerntechnischen Anlagen
4.2.1 Sellafield
In einer retrospektiven Kohortenstudie bei 260 060 Einzelgeburten (also keine Mehrlingsgeburten, aber auch Totgeburten) im Zeitraum 1950 bis 1989 in Cumbria, England, wurde untersucht, ob sich das Geschlechtsverhältnis (Jungen : Mädchen) der Nachkommen von Vätern, die jemals in der Wiederaufbereitungsanlage Sellafield11 beschäftigt waren, unterscheidet von dem der Väter, die nie dort arbeiteten (Dickinson et al. 1996). Das Geschlechtsverhältnis der 16 039 Geburten bei Vätern, die jemals in Sellafield beschäftigt waren, betrug 1,094 (95 %-KI: 1,060 – 1,128), das der 244 021 Geburten bei niemals in Sellafield beschäftigten Vätern 1,055 (95 %-KI: 1,046 – 1,063), d. h. bei den jemals in Sellafield Beschäftigten wurden relativ mehr Jungen geboren. Dieser Unterschied ist nicht signifikant. Bei den Vätern, die in den 90 Tagen vor Konzeption eine Dosis vom mehr als 10 mSv erhielten, war das Geschlechtsverhältnis auf der Basis von 345 Geburten hin zu einem größeren Anteil von Knabengeburten statistisch signifikant verschoben, nämlich auf 1,396 (95 %-KI: 1,127 – 1,729). Allerdings konnte keine Dosis-Wirkungs-Beziehung festgestellt werden. Bezüglich des erhöhten Geschlechtsverhältnisses bei den in Sellafield Beschäftigten weisen die Autoren der Studie darauf hin, dass diese Väter jünger waren als die nie in Sellafield Beschäftigten und dass das Geschlechtsverhältnis mit zunehmendem Alter des Vaters abnimmt.
Die Autoren diskutieren weiter, dass der Befund für Dosen über 10 mSv in den letzten 90 Tagen vor Konzeption möglicherweise auf Fehlklassifikation der Dosen oder auf multiples Testen zurückzuführen sein könnte. Allerdings ist auch eine tatsächliche statistische Assoziation nicht auszuschließen. Der Befund des veränderten Geschlechtsverhältnisses konnte nicht gezeigt werden, wenn statt der Dosis in den letzten 90 Tagen vor Konzeption die insgesamt akkumulierte Dosis berücksichtigt wird. Ferner weisen die Autoren darauf hin, dass es in Cumbria zufällig Extremwerte für das Geschlechtsverhältnis im Zeitraum 1959 bis 1960 und 1983 bis 1985 gab.
4.2.2 Andere Anlagen
In einer anderen Studie wurde das Geschlechtsverhältnis bei mehr als 46 000 Lebendgeburten untersucht, wobei die Exposition sowohl für männliche als auch für weibliche Beschäftigte berücksichtigt werden konnte (Maconochie et al. 2001). Die Studienpopulation umfasste Beschäftigte von Nuclear Weapons Establishment, Atomic Energy Authority und von British Nuclear Fuels. Informationen zu den Geburten wurden über eine schriftliche Befragung erhoben, für die der Rücklauf mit 82 % bei männlichen und 88 % bei weiblichen Beschäftigten sehr gut war. Die lebenslange berufliche Strahlenexposition wurde über die entsprechenden jährlichen Aufzeichnungen erfasst. Das Geschlechtsverhältnis wurde verglichen mit dem der Gesamtbevölkerung von England und Wales.
Unter den 39 502 lebendgeborenen Nachkommen von 18 131 männlichen Beschäftigen waren 20 346 männlich. Das Geschlechtsverhältnis von 1,06 entsprach dem der Gesamtbevölkerung. Ferner war das Geschlechtsverhältnis bei den Kindern, bei den die Konzeption vor Beschäftigungsbeginn lag, identisch mit dem der Kinder mit einem Konzeptionstermin nach Beschäftigungsbeginn.
Ebenfalls bei den 8 883 Lebendgeburten der 4 435 weiblichen Beschäftigten gab es keine Unterschiede im Geschlechtsverhältnis der Neugeborenen gegenüber der Vergleichsbevölkerung. Es gab auch keinen Hinweis darauf, dass sich das Geschlechtsverhältnis unterschied bei den Müttern, die vor Konzeption einer Strahlenüberwachung unterlagen.
Verglichen mit dem Geschlechtsverhältnis der Nachkommen bei den männlichen Beschäftigten lag das bei den weiblichen Beschäftigten statistisch unauffällig niedriger (OR=0,98, 95 %-KI: 0,94 – 1,02).
In keiner der untersuchten Gruppen zeigte sich ein Zusammenhang zwischen dem Geschlechtsverhältnis und der Höhe der Strahlenexposition, die in der am höchsten exponierten Gruppe über 50 mSv lag.
4.3 Bewohner der Umgebung des Atomwaffentestgeländes in Kasachstan
Eine Kohortenstudie wurde bei Bewohnern der Umgebung des Atomwaffentestgeländes in Kasachstan durchgeführt. Die Strahlenexposition wurde für jedes Kohortenmitglied abgeschätzt, und es wurden weitere Daten auf individueller Ebene sowohl für die Mütter als auch für die Väter berücksichtigt (Mudie et al. 2007). Insgesamt gingen 11 464 Einzelgeburten von 3 992 exponierten Müttern in die Analyse ein. Die Geburten fanden zwischen 1949 und 1956 statt.
Das Geschlechtsverhältnis lag bei 1,07. Bei den 1 402 Müttern mit einer Dosis von weniger als 200 mSv lag das Geschlechtsverhältnis auf der Basis von 3 548 Geburten bei 1,04 (95 %-KI: 0,97 – 1,11), bei den 707 Müttern mit einer Exposition über 600 mSv auf der Basis von 2 227 Geburten bei 1,12 (95 %-KI: (1,03 – 1,22). In der Dosisklasse 200 mSv bis 399 mSv betrug das Geschlechtsverhältnis auf der Basis von 2 879 Geburten durch 1 053 Mütter 1,05 (95 %-KI: 0,98 – 1,12), in der Dosisklasse 400 mSv bis 599 mSv bei 2 810 Geburten durch 830 Mütter 1,08 (95 %-KI: 1,00 – 1,16). Allerdings lag keine statistisch signifikante Dosis-Wirkungs-Beziehung vor. Das Geschlechtsverhältnis war assoziiert mit dem Alter der Mutter und der Geburtenfolge. Der Jungenanteil stieg (signifikant bzw. fast signifikant) mit dem Alter der Mutter bzw. des Vaters, dies steht im Gegensatz zu den Beobachtungen in den in den Abschnitten 3.3 und 4.2 besprochenen Arbeiten. Ein Einfluss der ethnischen Zugehörigkeit wurde diskutiert, konnte aber nicht statistisch signifikant nachgewiesen werden. Väterliche Faktoren hatten nur einen geringen bis keinen Einfluss auf das Geschlechtsverhältnis. Die Autoren kommen zusammenfassend zu dem Schluss, dass es keinen signifikanten Zusammenhang zwischen dem Geschlechtsverhältnis und der Strahlenexposition gibt, wohl aber zwischen dem Geschlechtsverhältnis und anderen diskutierten demografischen Faktoren.
Hinsichtlich der Expositionsabschätzung ist festzustellen, dass hier die Dosen überschätzt wurden (vergleiche Grosche et al. 2011). Welchen Einfluss die aktuelle Dosimetrie auf das Ergebnis hat, kann derzeit nicht geprüft werden.
Bei einer Analyse des Geschlechtsverhältnisses in Abhängigkeit von der Zeit seit Exposition betrug das Verhältnis für die ersten vier Jahre nach Exposition 0,99 (auf der Basis von 1 041 Geburten), für 5 bis 9 Jahre nach Exposition 1,02 (2 760), 10 bis 14 Jahre nach Exposition 1,08 (3 281), 15 bis 19 Jahre nach Exposition 1,16 (2 203) und bei 20 Jahren und mehr nach Exposition 1,04 (2 179), ein Trend war nicht erkennbar (ptrend = 0.35).
4.4 Übersicht über die erwähnten und weitere Studien
Für alle in den Abschnitten 4.1 bis 4.3 aufgeführten Studien gilt, dass sie neben der Strahlenexposition weitere Risikofaktoren berücksichtigt haben. Schull et al. (1966) berücksichtigten das Verwandtschaftsverhältnis zwischen den Eltern, während bei der Analyse von Yoshimoto et al. (1991) Informationen zu Geburtenfolge, Dauer der Schwangerschaft und Geburtsgewicht für jene 41 649 der insgesamt 72 228 (57,7 %) Geburten vorlagen, die zwischen 1948 und 1958 stattfanden. Dickinson et al. (1996) haben in ihren Analysen den Sozialstatus mit berücksichtigt sowie Geburtsjahr, Alter des Vaters und Geburtenfolge. Maconochie et al. (2001) haben das Geburtsjahr in der Analyse berücksichtigt, während Mudie et al. (2007) eine ganze Reihe möglicher Risikofaktoren in die Analysen haben einfließen lassen: ethnische Zugehörigkeit der Mutter, Schulabschluss der Mutter und des Vaters, Alter der Mutter und des Vaters zum Zeitpunkt der Geburt, Geburtenfolge und Jahreszeit zum Zeitpunkt der Geburt. Ein signifikanter Zusammenhang bestand dabei zwischen dem Geschlechtsverhältnis und dem Alter der Mutter und der Geburtenfolge.
Scherb und Voigt (2011) berichten über eine Veränderung des Geschlechtsverhältnisses (sex odds) bei den Lebendgeburten nach Tschernobyl und sagen, dass relativ kurze Zeit nach der Reaktorkatastrophe in Tschernobyl in 39 Staaten Westeuropas ein deutliches Abweichen des Geschlechtsverhältnisses von einem langjährigen Trend zu beobachten sei. Ein solches Abweichen sei in den USA nicht zu beobachten. Sie führen dies auf die zusätzliche Strahlenexposition nach dem Reaktorunfall zurück.
Das Geschlechtsverhältnis ändert sich hin zu einem höheren Anteil von Jungen, d. h. es werden relativ weniger Mädchen geboren als auf Grund des langjährigen Trends zu erwarten wären.
Bei der Betrachtung von Scherb und Voigt handelt es sich um eine ökologische Analyse, die es nicht erlaubt, die individuelle Strahlenexposition der Eltern der Kinder zu berücksichtigen. Solche ökologischen Analysen bergen das Risiko fehlerhafter Interpretation (ecological fallacy).
Scherb und Voigt (2011) betrachten in ihrer Analyse kurze Zeiträume nach Exposition und beschreiben eine Verschiebung des Geschlechtsverhältnisses hin zu einem größeren Anteil an Jungen im Jahr nach dem Tschernobyl-Unfall. Aus den in den Abschnitten 4.1 bis 4.3 diskutierten Studien ergibt sich hinsichtlich der Zeit nach Exposition ein uneinheitliches Bild. Während Schull und Neel (1958) sich hierzu vorsichtig äußern, zeigt sich bei Dickinson et al. (1996) ein Effekt bei 90 Tagen nach Exposition, während Maconochie et al. (2001) keinen Effekt sehen und Mudie et al. (2007) keinen Trend sehen.
Im Anhang werden die Ergebnisse der in den Abschnitten 4.1 bis 4.3 erwähnten sowie weiterer Studien wiedergegeben. Dabei zeigt sich, dass im Zusammenhang mit präkonzeptioneller Strahlenexposition der Väter Veränderungen des Geschlechtsverhältnisses in beide Richtungen beobachtet wurden. Auffällig ist, dass die Mehrzahl der Studien in den 1950er und 60er Jahren publiziert wurde. Der Grund für diese Häufung liegt vermutlich in der seinerzeit diskutierten Bedeutung der genetisch signifikanten Dosis.
In einer Übersichtsarbeit von 2011 gehen Terrell et al. (2011) der Frage nach, ob und wenn ja welche Umweltfaktoren auf der Basis bisher vorliegender Studien konsistent mit einer Veränderung des Geschlechtsverhältnisses – unabhängig von der Richtung der Veränderung – in Verbindung gebracht werden. Sie kommen zu dem Schluss, dass für väterliche Expositionen dies nur für Dioxine und Polychlorierte Biphenyle der Fall ist. Terrell et al. (2011) zeigen darüber hinaus, dass es bei sieben Studien an Personen, die auf Grund einer Tumorerkrankung einer Strahlentherapie unterzogen wurden, keinen Hinweis auf eine Veränderung des Geschlechtsverhältnisses gibt. Diese Studien sind allerdings wegen der Höhe der Strahlenexposition und der Zeit zwischen Exposition und Konzeption im Zusammenhang mit den hier diskutierten niedrigen Expositionen und relativ kurzen Zeiten zwischen Exposition und Konzeption nicht einzeln aufgeführt.
Auf eine ausführliche Darstellung aller im Anhang aufgeführten Studien wurde verzichtet, da es sich bei den meisten Arbeiten um Studien aus den 1950 bis 1960er Jahren handelt und die Ergebnisse, insbesondere im Zusammenhang mit beruflicher Exposition der Ärzte, aufgrund ihrer Datenerhebungsstrategie teilweise niedrige Rücklaufquoten oder einen geringen Studienumfang haben.
4.5 Biologischer Aspekt
Die der Arbeit von Scherb und Voigt (2011) zugrunde liegende Hypothese lautet, dass bestrahlte Männer eher Jungen als Mädchen zeugen (James 1997). Andererseits würden bestrahlte Mütter mehr Mädchen als normal zur Welt bringen (Schull und Neel 1958). In einer Antwort auf James (1997), der sich zur Arbeit von Dickinson et al. (1996) äußert, stellen diese fest, dass Schull und Neel ihre Theorie von 1958 später revidiert haben (siehe dazu auch Abschnitt 4.1): „As knowledge of genetics progressed, Schull and Neel reconsidered this theory, their most recent postulate being that while maternal exposure would, in principle, reduce the sex ratio, it is difficult to predict what effect irradiation of fathers might have since, with the recognition that one X chromosome is inactive in the somatic cells of women (the Lyonization phenomenon), it became clear that sex linked mutations induced in males were unlikely to have a dominant lethal effect in females ..“ (Dickinson et al. 1997).
In einer Replik auf die Arbeit von Scherb und Voigt (2011) weisen Bochud und Jung (2012) ferner darauf hin, dass das Geschlechtsverhältnis in den ersten Tagen der Embryogenese deutlich von dem eigentlich zu erwartenden 1:1-Verhältnis abweicht und Werte von bis zu 1,7 erreichen kann. Während der Gestation fände dann ein kontinuierliches Absinken dieses Geschlechtsverhältnisses statt hin zu den bei Geburt beobachteten Werten. Offensichtlich unterliegen männliche Embryonen und Föten einem höheren pränatalen Mortalitätsrisiko als weibliche. Verschiebungen des Geschlechtsverhältnisses hin zu einem höheren Anteil von Jungen könnten also auch als eine Reduktion des Verlustes männlicher Embryonen interpretiert werden.
4.6 Zusammenfassung
Während bei den Überlebenden der Atombombenabwürfe eine Verschiebung des Geschlechtsverhältnisses eher hin zu einem höheren Anteil von Mädchen berichtet wird, könnten die Ergebnisse von Dickinson et al. (1996) und Mudie et al. (2007) mit Vorsicht in Richtung auf eine Verschiebung hin zu einem geringeren Anteil von Mädchen angesehen werden. Allerdings wurde in keiner dieser beiden Arbeiten eine Dosis-Wirkungs-Beziehung beobachtet.
Somit ordnen sich diese Arbeiten gut in das Bild ein, das sich schon aus früheren Studien ergeben hat und die im Anhang dargestellt werden, d. h. es ergibt sich ein uneinheitliches Bild.
5 Methodische Bedingungen
5.1 Untersuchungen an Tieren und Vergleiche mit Studien am Menschen
Das Geschlecht der Nachkommen wird bei vielen Tierarten nicht allein durch genetische Faktoren bestimmt, sondern ist von weiteren Faktoren abhängig. In extremer Form ist dies bei einigen Reptilien der Fall, da der bestimmende Außenfaktor für das Geschlecht die Temperatur ist, der die Eier ausgesetzt sind. Bei Säugern ist die Geschlechtsdetermination zwar primär chromosomal, dennoch sind auch hier Außenfaktoren (insbesondere Temperatur, Ernährung und sozialer Status) in der Lage, das Geschlecht der Nachkommen zum Teil deutlich zu beeinflussen.
Die nichtchromosomale Beeinflussung des Geschlechts hat vermutlich einen evolutionären Hintergrund, da die Weitergabe der eigenen Gene in die übernächste Generation (F2) stark von der reproduktiven Fitness der Nachkommen (F1) abhängt. Diese Theorie, zuerst formuliert von Trivers und Willard (1973), hat sich in vielen Bereichen als zutreffend erwiesen, während sie für den Menschen zum Teil zuzutreffen scheint (Temperatur und Geschlechtsverhältnis), zum Teil aber auch im Widerspruch zu der Theorie steht (Ernährungslage und Geschlechtsverhältnis). So ist es bei vielen Tierarten und günstiger Ernährungslage besser, männliche Nachkommen zu produzieren, da diese im späteren Konkurrenzkampf um Weibchen bessere Chancen haben sich fortzupflanzen. Bei schlechter Ernährungslage ist es besser, keine männlichen, sondern weibliche Nachkommen zu produzieren, da sie ihrerseits ohnehin Nachkommen bekommen werden.
Die „Trivers-Willard-Hypothese“ ist auch in anderen Zusammenhängen geeignet, nicht-chromosomale Einflüsse auf das Geschlecht im evolutionsbiologischen Kontext als sinnvoll erscheinen zu lassen, wenngleich die biologischen Mechanismen nach wie vor unklar sind. So konnte beispielsweise gezeigt werden, dass niedrige Umgebungstemperaturen – als Merkmal „schlechter Zeiten“ – in Ratten und Fledermäusen zu sehr deutlichen Verschiebungen der Geschlechtsverhältnisse führen: Wurden Ratten über 5 Generationen bei 5° C gehalten, war das Geschlechtsverhältnis 0,74 gegenüber 1,07 bei Kontrolltieren (22° C) (Moriya und Hiroshige 1978). Auch bei Untersuchungen an freilebenden Fledermäusen konnte gezeigt werden, dass hohe Temperaturen das Geschlechtsverhältnis hin zu mehr männlichen Nachkommen verschieben (Ransome und McOwat 1994). In die gleiche Richtung weisen auch statistische Untersuchungen von Geburten in Deutschland, bei denen die monatlichen Temperaturen und die Abweichungen gegenüber den langjährigen Mittelwerten mit den jeweiligen Geschlechtsverhältnissen verglichen wurden (Lerchl 1999). Auch hier zeigten sich, wenngleich weit weniger deutlich, signifikante Effekte, die darauf hindeuten, dass höhere Temperaturen ein bis zwei Monate vor der Konzeption mit mehr Knabengeburten assoziiert sind. Weiterhin ist mehrfach berichtet worden, dass das Verhältnis von männlichen zu weiblichen Nachkommen bei Tieren und Menschen von der Jahreszeit abhängt (Lerchl 1998, Navara et al. 2010, Roche et al. 2006, Slatis 1953). Ob diese Effekte von der Photoperiode abhängen oder von der Temperatur, ist unklar.
Weitere Einflussgrößen auf das Geschlechtsverhältnis sind der soziale Status und die Populationsdichte (Springböcke: Krüger et al. 2005, Rotwild: Kruuk et al. 1999, Mäuse: Krackow et al. 1997) sowie die Konzentrationen von Hormonen wie Steroide und Glucocorticoide (z. B. James 2008). Inwieweit sich diese Faktoren hinsichtlich des Einflusses auf das Geschlechtsverhältnis gegeneinander abgrenzen lassen, wird derzeit intensiv diskutiert (Übersicht bei Helle et al. 2013), insbesondere für den Faktor „Stress“, der sich hinsichtlich der Richtung des Effekts hin zu mehr weiblichen Nachkommen als sehr robust erweist. Dies gilt nicht nur für viele Untersuchungen an Tieren (Übersicht bei Ryan et al. 2012), sondern scheint sich auch bei Menschen zu bestätigen, wie Untersuchungen nach Erdbeben (Fukuda et al. 1998, Saadat 2008) und nach dem Anschlag vom 11. September 2001 in New York (Catalano et al. 2006) zeigten (siehe Abschnitt 3.1).
Verschiedene chemische Substanzen, die im Verdacht stehen, das Geschlechtsverhältnis Neugeborener zu verändern, wurden in Tierversuchen getestet. So konnten Ishihara et al. (2007) mit sehr hohen Dosen von TCDD (2,3,7,8-Tetrachlordibenzodioxin, das so genannte „Seveso-Dioxin“) bei Männchen eine geringere Anzahl männlicher Nachkommen verursachen als in der Kontrollgruppe. In Folgeversuchen konnte gezeigt werden, dass bei gleicher Dosierung die Anzahl Spermien deutlich reduziert war und interessanterweise das Verhältnis von männlichen zu weiblichen Embryonen im Zweizellstadium (also vor der Einnistung) in der gleichen Größenordnung reduziert war wie das der ausgetragenen Tiere (Ishihara et al. 2010).
Für die möglichen Effekte ionisierender Strahlung auf das Geschlechtsverhältnis von Ratten gibt es eine ältere, allerdings umfangreiche Studie (Havenstein et al. 1968). Insgesamt wurde das Geschlecht von etwa 50 000 Ratten untersucht. Männliche oder weibliche Tiere wurden im Alter von 10, 12 und 14 Wochen exponiert (insgesamt 450 r Gammastrahlung12) und im Alter von 26 Wochen verpaart. Die männlichen (von bestrahlten Männchen) bzw. weiblichen (von bestrahlten Weibchen) Nachkommen wurden wiederum wie die Elterntiere bestrahlt und verpaart, der Versuch wurde bis in die 12. Generation fortgeführt. Insgesamt ergaben sich für die Versuche weder für die Bestrahlung der Männchen noch der Weibchen signifikante Effekte auf das Geschlechtsverhältnis der Nachkommen: „The difference between the control and irradiated groups, within generation and mating system, in the percentages of males was not significant except in one comparison in each of the two sub-experiments – a frequency of significant differences no greater than would be expected by chance with the probability levels involved.“
Eine kleinere Studie (Iwasaki et al. 1996) fand ebenfalls keine Effekte einer Gammastrahlen-Exposition (3 Gray) von Männchen auf das Geschlechtsverhältnis der Nachkommen.
6 Zusammenfassung und Schlussfolgerungen
- 1.
-
Das amtlich ermittelte Geschlechtsverhältnis der Lebendgeborenen wird potentiell durch eine Fülle möglicher Faktoren beeinflusst:
- –
-
endogene Faktoren, erworbene wie genetische,
- –
-
exogene Faktoren, individuell steuerbare und extern vorgegebene,
- –
-
statistische und forensische Faktoren.
- 2.
-
Die Wirkung dieser Faktoren kann sich zu unterschiedlichen Zeitpunkten entfalten:
- –
-
präkonzeptionell,
- –
-
während der Schwangerschaft,
- –
-
unter und nach der Geburt.
- 3.
-
Das Geschlechtsverhältnis wird bei vielen Tierarten zum Teil ausschließlich über Außenfaktoren bestimmt. Bestes Beispiel dürften Reptilien sein, deren Geschlecht durch die Temperatur determiniert wird, die auf die Eier einwirkt – höhere Temperaturen resultieren in Männchen. Aber auch für andere Wirbeltiere (Vögel, Säuger) ist bekannt, dass Außenfaktoren (gute Ernährung, höhere Temperatur, aber auch hoher sozialer Status) das Geschlecht der Nachkommen zum Teil deutlich hin zu männlichen Nachkommen verschiebt. Die so genannte Trivers-Willard-Hypothese generalisiert diese Beeinflussungen und postuliert einen evolutionsbiologischen Vorteil, bei günstigen Bedingungen eine Verschiebung hin zu männlichen Nachkommen zu ermöglichen, da diese im späteren Konkurrenzkampf um Weibchen einen Vorteil haben, während dieser Vorteil bei Weibchen nicht existiert. Die zellbiologischen bzw. genetischen Mechanismen hierfür sind unbekannt. Gammastrahlung (Havenstein et al. 1968) verursachte in Ratten über mehrere Generationen keine Veränderung des Geschlechtsverhältnisses.
- 4.
-
Untersuchungen am Menschen weisen z. T. auf den ersten Blick beeindruckende Fallzahlen auf, wenn es sich um die sekundärstatistische Auswertung amtlicher Daten zu Geburten handelt. Diesen Studien mangelt es allerdings regelhaft an der auch nur ansatzweise adäquaten Einbeziehung der unter Nummer 1 benannten Faktoren. Selbst der in den Studien jeweils untersuchte Zielrisikofaktor kann nur auf ökologischem Niveau gemessen werden und entbehrt damit einer zeitlichen Einordnung gemäß Nummer 2. Erschwerend kommt hinzu, dass das Geschlechtsverhältnis einen jahreszeitlichen Rhythmus zeigt und darüber hinaus auf Bevölkerungsniveau eine statistische Extravariation aufweist, deren Ursache als ungeklärt angesehen werden muss. Am ehesten scheint plausibel zu sein, dass in Not- und Kriegszeiten das Geschlechtsverhältnis der Lebendgeborenen zugunsten des Anteils an Knabengeburten erhöht ist. Woran das liegen mag, muss als ungeklärt betrachtet werden. Diese Studien erfüllen allesamt nicht die üblichen Kausalitätskriterien, die heutzutage an epidemiologische Studien gestellt werden. Umgekehrt weisen die analytisch-epidemiologischen Studien nicht die Fallzahl auf, die notwendig ist, einen solch relativ kleinen „Risikounterschied“ mit der erforderlichen statistischen Genauigkeit zu entdecken.
- 5.
-
Während bei den Überlebenden der Atombombenabwürfe eine Verschiebung des Geschlechtsverhältnisses eher hin zu einem höheren Anteil von Mädchen berichtet wird, könnten die Ergebnisse von Dickinson et al. (1996) und Mudie et al. (2007) mit Vorsicht in Richtung auf eine Verschiebung hin zu einem geringeren Anteil von Mädchen angesehen werden. Allerdings wurde in keiner dieser beiden Arbeiten eine Dosis-Wirkungs-Beziehung beobachtet.Somit ordnen sich diese Arbeiten gut in das Bild ein, das sich schon aus früheren Studien ergeben hat und die im Anhang dargestellt werden, d. h. es ergibt sich ein uneinheitliches Bild.
- 6.
-
Das Phänomen der Variation des Geschlechtsverhältnisses der Lebendgeborenen hat Wissenschaftler seit langer Zeit beschäftigt. Einer Aufklärung sind sie bislang nicht wesentlich näher gekommen. Klar ist jedoch, dass immer kompliziertere statistische Verfahren die grundsätzliche Problematik der komplexen Ursache-Wirkungs-Beziehungen nicht beseitigen können. Vielmehr besteht die Gefahr, dass durch nicht mehr nachvollziehbare Datenanalysen und Datengrundlagen zusätzlich die Transparenz der Wissenschaft leidet.
- 7.
-
Abseits des grundsätzlichen wissenschaftlichen Erkenntnisinteresses und im Lichte des Problems der erforderlichen Fallzahl stellt sich die Frage nach der Public-Health-Relevanz einer Erhöhung des Geschlechtsverhältnisses von zum Beispiel 1 050 auf 1 060 durch einen bestimmten Faktor. Dieser „Befund“ einer Veränderung des Geschlechtsverhältnisses von 1 050 auf 1 060 kann nämlich bedeuten, dass auf 100 Mädchengeburten ein Mädchen „zu wenig“ geboren wird, aber auch, dass auf 100 Knaben einer „zu viel“ geboren wird. Dies zeigt, dass aus Public-Health-Sicht eine Fokussierung auf den Parameter „Geschlechtsverhältnis der Lebendgeborenen“ nicht zielführend ist. Wollte man genaueres über die Wirkung dieses Faktors erfahren, müsste man ein systematisches Forschungsprogramm darüber auflegen, welche Wirkungen der Faktor auf die Zahl der Konzeptionen, der Schwangerschaftsabbrüche und der Geburten sowie die sonstigen putativen Risikofaktoren in den verschiedenen Phasen (vergleiche Nummer 2) entfaltet.
7 Literatur
- Barber 2004
-
Barber N. Sex ratio at birth, polygyny, and fertility: a cross-national study. Soc Biol. 2004 Spring-Summer; 51(1-2): 71-77.
- BiB 2012
-
Bundesinstitut für Bevölkerungsforschung (BiB). Lebendgeburt, Totgeburt und Fehlgeburt. http://www.bib-demografie.de/SharedDocs/Glossareintraege/DE/L/lebendgeburt.html (zuletzt aufgerufen 3. November 2014).
- Biggar et al. 1999
-
Biggar RJ, Wohlfahrt J, Westergaard T, Melbye M. Sex ratios, family size, and birth order. Am J Epidemiol. 1999 Nov; 150(9): 957-962.
- BMJ 2011
-
Bundesministerium für Justiz (BMJ). Personenstandsverordnung vom 22. November 2008 (BGBl. I S. 2263), die zuletzt durch Artikel 2 Absatz 8 des Gesetzes vom 22. Dezember 2011 (BGBl. I S. 3044) geändert worden ist.
- Bochud und Jung 2012
-
Bochud F, Jung T. Comment on the human sex odds at birth after the atmospheric atomic bomb tests, after Chernobyl, and in the vicinity of nuclear facilities (Hagen Scherb & Kristina Voigt. Environ, Sci Pollut Res. 2011 18: 697-707) Environ Sci Pollut Res Int. 2012 Jul; 19(6): 2456-2459.
- Bromen und Jöckel 1997a
-
Bromen K, Jöckel KH. Change in male proportion among newborn infants (Letter). Lancet 1997 Mar; 349(9054): 804-805.
- Bromen und Jöckel 1997b
-
Bromen K, Jöckel KH. Change in the male proportion among newborn and stillborn infants in Germany. In : Muche RI, Büchele G, Harder D, Gaus W (Hrsg.). Medizinische Informatik, Biometrie und Epidemiologie. 42. Jahrestagung der GMDS 1997. MMV Medizin Verlag 1997: 532-535.
- Catalano 2003
-
Catalano RA. Sex ratios in the two Germanies: a test of the economic stress hypothesis. Hum Reprod. 2003 Sep; 18(9): 1972-1975.
- Catalano et al. 2005
-
Catalano R, Bruckner T, Hartig T, Ong M. Population stress and the Swedish sex ratio. Paediatr Perinat Epidemiol. 2005 Nov; 19(6): 413-420.
- Catalano et al. 2006
-
Catalano R, Bruckner T, Marks AR, Eskenazi B. Exogenous shocks to the human sex ratio: the case of September 11, 2001 in New York City. Hum Reprod. 2006 Dec; 21(12): 3127-3131.
- Catalano und Bruckner 2005
-
Catalano RA, Bruckner T. Economic antecedents of the Swedish sex ratio. Soc Sci Med. 2005 Febr; 60(3): 537-543.
- Davis et al. 1998
-
Davis DL, Gottlieb MB, Stampnitzky JR. Reduced ratio of male to female births in several industrial countries: a sentinel health indicator? JAMA. 1998 Apr; 279(13): 1018-1023.
- Dean et al. 2010
-
Dean JH, Chapman MG, Sullivan EA. The effect on human sex ratio at birth by assisted reproductive technology (ART) procedures – an assessment of babies born following single embryo transfers, Australia and New Zealand, 2002-2006. BJOG. 2010 Dec; 117(13): 1628-1634.
- Dickinson et al. 1996
-
Dickinson HO, Parker L, Binks K, Wakeford R, Smith J. The sex ratio of children in relation to paternal preconceptional radiation dose: a study in Cumbria, northern England. J Epidemiol Community Health. 1996 Dec; 50(6): 645-652.
- Dickinson et al. 1997
-
Dickinson HO, Parker L, Binks K, Wakeford R. Reply to James WH on Ionizing radiation and offspring ratio. J Epidemiol Community Health. 1997; 51: 341-342.
- EC 2003
-
Europäische Kommission (EC). Eurostat. Bevölkerungsstatistik: Definitionen und Methoden zur Erhebung in 31 europäischen Ländern. Luxemburg: Amt für amtliche Veröffentlichungen der Europäischen Gemeinschaften, 2003.
- Fellman und Eriksson 2011
-
Fellman J, Eriksson AW. Temporal trends in the secondary sex ratio in Nordic countries. Biodemography Soc Biol. 2011; 57(2): 143-154.
- Fukuda et al. 1998
-
Fukuda M, Fukuda K, Shimizu T, Møller H. Decline in sex ratio at birth after Kobe earthquake. Hum Reprod. 1998 Aug; 13(8): 2321-2322.
- Gardner et al. 1990
-
Gardner MJ, Snee MP, Hall AJ, Powell CA, Downes S, Terrell JD. Results of case-control study of leukaemia and lymphoma among young people near Sellafield nuclear plant in West Cumbria. BMJ. 1990 Febr; 300: 423-429.
- Grosche et al. 2011
-
Grosche B, Lackland DT, Land CE, Simon SL, Apsalikov KN, Pivina LM, Bauer S, Gusev BI. Mortality from cardiovascular diseases in the Semipalatinsk historical cohort, 1960-1999, and its relationship to radiation exposure. Radiat Res. 2011 Nov; 176(5): 660-669.
- Hama et al. 2001
-
Hama Y, Uematsu M, Sakurai Y, Kusano S. Sex ratio in the offspring of male radiologists. Acad Radiol. 2001 May; 8(5): 421-424.
- Hassold et al. 1983
-
Hassold T, Quillen SD, Yamane JA. Sex ratio in spontaneous abortions. Ann Hum Genet. 1983 Jan; 47(Part 1): 39-47.
- Havenstein et al. 1968
-
Havenstein GB, Taylor BA, Hansen JC, Morton NE, Chapman AB. Genetic effects of cumulative X irradiation on the secondary sex ratio of the laboratory rat. Genetics. 1968 Jun; 59(2): 255-274. http://www.genetics.org/content/59/2/255.long (zuletzt aufgerufen 3. November 2014).
- Helle et al. 2013
-
Helle S, Laaksonen T, Huitu O. Sex-specific offspring growth according to maternal testosterone, corticosterone, and glucose levels. Behav Ecol. 2013; 24(1): 205-212.
- INSEE 2013a
-
Institut national de la statistique et des études économiques (INSEE). Stillbirth Definition. http://www.insee.fr/en/methodes/default.asp?page=definitions/enfant-sans-vie.htm (zuletzt aufgerufen 3. November 2014).
- INSEE 2013b
-
Institut national de la statistique et des études économiques (INSEE). Birth Definition. http://www.insee.fr/en/methodes/default.asp?page=definitions/naissance.htm (zuletzt aufgerufen 3. November 2014).
- Ishihara et al. 2007
-
Ishihara K, Warita K, Tanida T, Sugawara T, Kitagawa H, Hoshi N. Does paternal exposure to 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD) affect the sex ratio of offspring? J Vet Med Sci. 2007 Apr; 69(4): 347-52.
- Ishihara et al. 2010
-
Ishihara K, Ohsako S, Tasaka K, Harayama H, Miyake M, Warita K, Tanida T, Mitsuhashi T, Nanmori T, Tabuchi Y, Yokoyama T, Kitagawa H, Hoshi N. When does the sex ratio of offspring of the paternal 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD) exposure decrease: in the spermatozoa stage or at fertilization? Reprod Toxicol. 2010 Jan; 29(1): 68-73.
- Iwasaki et al. 1996
-
Iwasaki T, Hashimoto N, Endoh D, Imanisi T, Itakura C, Sato F. Life span and tumours in the first-generation offspring of the gamma-irradiated male mouse. Int J Radiat Biol. 1996 Apr; 69(4): 487-492.
- Jacobsen et al. 1999
-
Jacobsen R, Moller H, Mouritsen A. Natural variation in the human sex ratio. Human reproduction. 1999; 14(12): 3120-3125.
- James 1997
-
James WH. Ionizing radiation and offspring sex ratio. J Epidemiol Community Health. 1997 Jun; 51(3): 340-341.
- James 2008
-
James WH. Evidence that mammalian sex ratios at birth are partially controlled by parental hormone levels around the time of conception. J Endocrinol. 2008 Jul; 198(1): 3-15.
- Jöckel und Bromen 2000
-
Jöckel KH, Bromen K. Re: „Sex ratios, family size and birth order“. Letters to the Editor. Am J Epidemiol. 2000 Jun; 151(11): 1133-1134.
- Jöckel und Pflaumer 1981
-
Jöckel KH, Pflaumer P. Demographische Anwendungen neuerer Zeitreihenverfahren. Zeitschrift für Bevölkerungswissenschaft. 1981; 7: 519-542.
- Kitabake 1960
-
Kitabatake T. Sterility, stillbirth, infant death and sex ratio of offspring of X-ray workers. Nagoya J Med Sci. 1960; 2: 226-237.
- Krackow et al. 1997
-
Krackow S. Effects of mating dynamics and crowding on sex ratio variance in mice. J Reprod Fertil. 1997; 110: 87-90.
- Kriener 2012
-
Kriener M.: Die kubanische Mädchenlücke. taz vom 7. Oktober 12
- Krüger et al. 2005
-
Krüger O, Radford AN, Anderson C, Liversidge R. Successful sons or superior daughters: sex-ratio variation in springbok. Proc Biol Sci. 2005 Febr; 272(1561): 375-381.
- Kruuk et al. 1999
-
Kruuk LE, Clutton-Brock TH, Albon SD, Pemberton JM, Guinness FE. Population density affects sex ratio variation in red deer. Nature. 1999 Jun; 399(6735): 459-461.
- Lejeune et al. 1960
-
Lejeune PJ, Turpin R, Rethore MO. Les enfants nes de parents irradies (cas particular de la sex ratio). Proc of the IXth International Congress on Radiation, 1960: 1089-95.
- Lerchl 1998
-
Lerchl A. Seasonality of sex ratio in Germany. Human Reproduction. 1998; 13(5): 1401-1402.
- Lerchl 1999
-
Lerchl A. Sex ratios at birth and environmental temperatures. Naturwissenschaften. 1999 Jul; 86(7): 340-342.
- Luke et al. 2009
-
Luke B, Brown MB, Grainger DA, Baker VL, Ginsburg E, Stern JE, Society for Assisted Reproductive Technology Writing Group. The sex ratio of singleton offspring in assisted conception pregnancies. Fertil Steril. 2009 Nov; 92(5):1579-1585.
- Macht und Lawrence 1955
-
Macht SH, Lawrence PS. National survey of congenital malformations resulting from exposure to roentgen radiation. Am J Roentgenol Radium Ther Nucl Med. 1955 Mar; 73(3): 442-66.
- Maconochie et al. 2001
-
Maconochie N, Roman E, Doyle P, Davies G, Smith PG, Beral V. Sex ratio of nuclear industry employees’ children. Lancet. 2001 May; 357(9268): 1589-1591.
- Masuy-Stroobant 1997
-
Masuy-Stroobant G. Infant Health and Infant Mortality in Europe: Lessons from the Past and Challenges for the Future. In: Corsini CA, Viazzo PP (Hrsg.): The Decline of Infant and Child Mortality. The European Experience: 1750-1990. Den Haag: Kluwer Law International: 1-34.
- Mathews und Hamilton 2005
-
Mathews TJ, Hamilton BE. Trend analysis of the sex ratio at birth in the United States. Natl Vital Stat Rep. 2005 Jun; 53(20): 1-17.
- Moriya und Hiroshige 1978
-
Moriya K, Hiroshige T. Sex ratio of offsprings of rats bred at 5 degrees C. Int J Biometeorol. 1978 Dec; 22 (4): 312-315.
- Mudie et al. 2007
-
Mudie NY, Gusev BI, Pivina LM, Schoemaker MJ, Rijinkova ON, Apsalikov KN, Swerdlow AJ. Sex ratio in the offspring of parents with chronic radiation exposure from nuclear testing in Kazakhstan. Radiat Res. 2007 Nov; 168(5): 600-607.
- Müller et al. 1962
-
Müller C, Rericha V, Kubat M. Zur Frage der genetischen Auswirkung der ionisierenden Strahlung bei Joachimstaler Bergleuten. Zentralbl Gynaekol. 1962; 84: 558-560.
- Navara et al. 2010
-
Navara KJ, Workman JL, Oberdick J, Nelson RJ. Short day lengths skew prenatal sex ratios toward males in Siberian hamsters. Physiol Biochem Zool. 2010 Jan-Febr; 83(1): 127-134.
- Neel 1963
-
Neel JV. Changing perspectives on the genetic effects of radiation. Springfield, Ill.: Charles C Thomas, 1963.
- Neel et al. 1990
-
Neel JV, Schull WJ, Awa AA, Satoh C, Kato H, Otake M, Yoshimoto Y. The children of parents exposed to atomic bombs: estimates of the genetic doubling dose of radiation for humans. Am J Hum Genet 1990 Jun; 46(6): 1053-1072.
- Nierling 2008
-
Nierling U. Frühgeburten in Rostock – Eine retrospektive Analyse mit Erstellung eines Risikoprofils unter besonderer Berücksichtigung maternaler Faktoren. Inauguraldissertation zur Erlangung des akademischen Grades Doktor der Medizin der Medizinischen Fakultät der Universität Rostock, 2008.
- Ransome und McOwat 1994
-
Ransome RD, McOwat TP. Birth timing and population changes in greater horseshoe bat colonies (Rhinolophus ferrumequinum) are synchronized by climatic temperature. Zool J Linn Soc. 1994; 112(3): 337-351.
- Roche et al. 2006
-
Roche JR, Lee JM, Berry DP. Climatic factors and secondary sex ratio in dairy cows. J Dairy Sci. 2006 Aug; 89(8): 3221-7.
- Ryan et al. 2012
-
Ryan CP, Anderson WG, Gardiner LE, Hare JF. Stress-induced sex ratios in ground squirrels: support for a mechanistic hypothesis. Behav Ecol. 2012; 23: 160-167.
- Saadat 2008
-
Saadat M. Decline in sex ratio at birth after Bam (Kerman Province, Southern Iran) earthquake. J Biosoc Sci. 2008; 40(6): 935-937.
- Scherb et al. 2013
-
Scherb H, Kusmierz R, Voigt K: Increased sex ratio in Russia and Cuba after Chernobyl: a radiological hypothesis. Environmental Health. 2013 Aug; 12: 63.
- Scherb und Voigt 2011
-
Scherb H, Voigt K. The human sex odds at birth after the atmospheric atomic bomb tests, after Chernobyl, and in the vicinity of nuclear facilities. Environ Sci Pollut Res Int. 2011 Jun; 18(5): 697-707.
- Schnettler und Klüsener 2013
-
Schnettler S, Klüsener S: economic stress or random variation? Revisiting german reunification as a natural experiment to investigate the effect of economic contraction on sex ratios at birth. MPIDR Working Paper WP 2013-005, May 2013, http://www.demogr.mpg.de/papers/working/wp-2013-005.pdf (zuletzt aufgerufen 3. November 2014).
- Scholte und Sobels 1963
-
Scholte PJL, Sobels FH. Sex ratio shifts among progeny from patients having received therapeutic X-radiation. Hum Genet. 1964; 16(1): 26-37.
- Schull 1958
-
Schull WJ. Empirical risks in consanguineous marriages: sex ratio, malformation, and viability. Am J Hum Genet. 1958 Sep; 10(3): 294-343.
- Schull et al. 1966
-
Schull WJ, Neel JV, Hashizume A. Some further observations on the sex ratio among infants born to survivors of the atomic bombings of Hiroshima and Nagasaki. Am J Hum Genet. 1966 Jul; 18(4): 328-338.
- Schull und Neel 1958
-
Schull WJ, Neel JV. Radiation and the sex ratio in man. Science. 1958 Aug; 128: 343-348.
- Simpson 2001
-
Simpson L. Reviews: The Human Dichotomy, the changing numbers of males and females by John Clarke. Radical Statistics 77, 2001 http://www.radstats.org.uk/no077/simpson.htm (zuletzt aufgerufen 4. November 2014).
- Simpson 2012
-
Simpson L. Re: „The association between living through a prolonged economic depression and the male:female birth ratio − A longitudinal study from Cuba, 1960 − 2008“ und „Invited commentary: Natural versus unnatural sex ratios − A quandary of modern times“. Letters to the Editor. Am J Epidemiol. 2012; 175(9): 973.
- Slatis 1953
-
Slatis HM. Seasonal variation in the American live birth sex ratio. Am J Hum Genet. 1953; 5: 21-33.
- StBA 1972
-
Statistisches Bundesamt. Bevölkerung und Wirtschaft 1872 − 1972. Stuttgart: Verlag W. Kohlhammer 1972. https://www.destatis.de/GPStatistik/servlets/MCRFileNodeServlet/DEMonografie_derivate_00000198/Bevoelkerung_und_%20Wirtschaft%201872_1972.pdf;jsessionid=9AA99CE399A461FB1A0CA2E0753FB1FE (zuletzt aufgerufen 3. November 2014).
- StBA 2012
-
Statistisches Bundesamt. Bevölkerung und Erwerbstätigkeit. Natürliche Bevölkerungsbewegung 2010. Fachserie 1 Reihe 1.1. Wiesbaden, 2012. https://www.destatis.de/DE/Publikationen/Thematisch/Bevoelkerung/Bevoelkerungsbewegung/Bevoelkerungsbewegung2010110127004.pdf?__blob=publicationFile (zuletzt aufgerufen 3. November 2014).
- Süßmilch 1765
-
Süßmilch JP. Die göttliche Ordnung in den Veränderungen des menschlichen Geschlechts, aus der Geburt, dem Tod und der Fortpflanzung desselben erwiesen. Zweyter Theil. (1765), Dritte und ganz umgearbeitete Auflage. Im Verlag des Buchladens der Realschule. Berlin. Nachdruck Jürgen Cromm Verlag, Göttingen, 1988.
- Tanaka und Okhura 1958
-
Tanaka K, Ohkura K. Evidence for genetic effects of radiation in offspring of radiological technicians. Jpn J Hum Genet. 1958; 3: 135-145.
- Tanaka und Okhura 1961
-
Tanaka K, Ohkura K. Genetic effects of radiation in man: a study of the sex-ratio in the offspring of radiological technicians. Proc of the Second International Conference on Human Genetics, 1961.
- Terrell et al. 2011
-
Terrell ML, Hartnett KP, Marcus M. Can environmental or occupational hazards alter the sex ratio at birth? A systematic review. Emerging Health Threats Journal. 2011; 4: 7109.
- Trivers und Willard 1973
-
Trivers RL, Willard DE. Natural selection of parental ability to vary the sex ratio of offspring. Science. 1973 Jan; 179(4068): 90-92.
- Turpin et al. 1956
-
Turpin R, Lejeune PJ, Rethore MO. Etude de la descendance de sujets traits par radiotherapie pelvinne. Acta Genet Stat Med. 1956; 6(2): 204-216.
- Van den Broek 1997
-
Van den Broek JM. Change in male proportion among newborn infants (Letter). Lancet. 1997 Mar; 349(9054): 805.
- Venero Fernández et al. 2011
-
Venero Fernández SJ, Medina RS, Britton J, Fogarty AW. The association between living through a prolonged economic depression and the male:female birth ratio − a longitudinal study from Cuba, 1960-2008. Am J Epidemiol. 2011 Dec; 174(12): 1327-1331.
- Venero Fernández et al. 2012
-
Venero Fernández SJ, Medina RS, Britton J, Fogarty AW. Reply to Simpson L (Re: „The association between living through a prolonged economic depression and the male: female birth ratio - a longitudinal study from Cuba, 1960 - 2008“ und „Invited commentary: Natural versus unnatural sex ratios - A quandary of modern times“. Am J Epidemiol. 2012; 175(9): 973). Am J Epidemiol. 2012; 175(9): 973-974.
- Yoshimoto et al. 1991
-
Yoshimoto Y, Schull WJ, Kato H, Neel JV. Mortality among the offspring (F1) of atomic bomb survivors, 1946-85. J Radiat Res. 1991 Dec; 32(4): 327-351.
- Zadeh und Briggs 1997
-
Zadeh HG, Briggs TW (1997) Ionising radiation: are orthopaedic surgeons’ offspring at risk? Ann R Coll Surg Engl. 1997 May; 79(3): 214-220.
Übersicht über Studien zum Geschlechtsverhältnis bei exponierten Vätern und/oder Müttern, unterschieden nach chronischer und akuter Strahlenexposition
| Referenz | Studienpopulation | Kinder Exponierter |
Kinder Kontrollen |
Geschlechtsverhältnis oder Anteil der Jungen (m) |
Dosis | Vergleich | Ergebnis | Hinweis |
|---|---|---|---|---|---|---|---|---|
| chronische Exposition | ||||||||
| Macht und Lawrence 1955 | Radiologen vs. andere Mediziner | N = 4 127 m = 2 090 w = 2 037 u = 592 |
N = 3 946 m = 1 766 w = 1 624 u = 556 |
Jungen pro 100 Mädchen: Kontr. 108,74 Exp. 102,60 |
unbekannt | Exponierte vs. Nicht- Exponierte Exponierte vs. Bevölkerungsdurchschnitt |
Verschiebung hin zu mehr Mädchen; insgesamt entspricht das Geschlechtsverhältnis dem Bevölkerungsdurchschnitt | Basis der Untersuchung ist eine Erhebung; Response bei Radiologen 74,1 %, bei anderen Ärzten 53,8 %; unbekanntes Geschlecht bei 15 % der Geburten |
| Tanaka und Okhura 1958, 1961 | radiologische Techniker vs. Krankenhaus-apotheker | N = 726 m = 377 w = 302 |
N = 963 m = 478 w = 431 |
Anteil der Jungen in %: Kontr. 52,6 % Exp. 55,5 % |
20 bis 50 r/a Ø (230 bis 575 r) akkumuliert in Ø 11,48 Jahren vor Konzeption |
Exponierte vs. Nicht- Exponierte Exponierte vs. Bevölkerungsdurchschnitt |
Verschiebung hin zu den Jungen, sowohl gegenüber der Kontrollgruppe als auch gegenüber der Allgemeinbevölkerung | Basis der Untersuchung ist eine Erhebung; Response bei radiologischen Technikern 78,2 %, bei Apothekern 56,0 %; fehlendes Geschlecht bei 5,6 % der Geburten |
| Kitabatake 1960 | 40 Radiologen, 203 Röntgen-techniker vs. 260 nicht strahlenexponierte Beschäftigte | N = 246 m = 131 w = 115 |
N = 287 m = 146 w = 141 |
Anteil der Jungen: Kontr. 0,5087 (±0,0120) Exp. 0,5325 (±0,0115) |
70 bis 1 000 r akkumulierte Dosis vor der Konzeption |
Exponierte vs. Nicht- Exponierte |
Verschiebung hin zu den Jungen Dosis-Wirkungs- Beziehung: höhere Dosis führt zu stärkerer Verschiebung des Geschlechtsverhältnisses hin zu den Jungen |
Basis der Untersuchung ist eine Erhebung; Response bei Radiologen und Technikern 67,1 %, bei anderen Beschäftigten 53,8 %; die Dosis wurde in Abhängigkeit der Filme und Durchleuchtungsstunden unter Berücksichtigung der technischen Entwicklung abgeschätzt |
| Müller et al. 1962 | Joachimsthaler Uranbergarbeiter; Geburten vor und nach Beschäftigungsbeginn | N = 716 m = 300 w = 386 |
N = 1 192 m = 618 w = 574 |
Jungen pro 100 Mädchen: vor Expositionsbeginn: 107,6 nach Expositionsbeginn: 85,4 |
unbekannt | vor vs. nach Aufnahme der Arbeit im Uranbergbau | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen | Die Verschiebung zeigt sich am deutlichsten in den ersten drei Jahren nach Expositionsbeginn |
| Zadeh und Briggs 1997 | Anteil m/w in %: Normalbevölkerung: 51 %/49 % |
unbekannt | mit der Allgemeinbevölkerung | der Anteil der Mädchengeburten lag höher als in der Allgemeinbevölkerung | Basis der Untersuchung ist eine schriftliche Befragung; Response bei den Chirurgen 66 %, in der Vergleichsgruppe 62 % | |||
| 216 (von 334) orthopädische Chirurginnen/Chirurgen mit Kindern | N = 451 | 47 %/53 % | ||||||
| 714 (von 986) Geburtshelferinnen/Geburtshelfer und Gynäkologinnen/Gynäkologen mit Kindern | N = 1 257 (mit Exposition) | N = 292 (ohne Exposition) | 49 %/51 % (keine Unterscheidung zwischen den beiden Expositionsgruppen) | |||||
| Hama et al. 2001 | 586 männliche Radiologen | N = 1 015 m = 492 w = 523 |
Geschlechtsverhältnis (m/w): 1,06 (in der Allgemeinbevölkerung) 0,94 (für alle Radiologen) 0,53 (für die Gruppe mit Exposition > ICRP- Empfehlung) |
über oder unter dem Wert der ICRP-Empfehlungen | mit der Allgemeinbevölkerung | der Anteil der Mädchengeburten lag höher als in der Allgemeinbevölkerung, und bei den hochexponierten höher als bei allen Radiologen zusammen | Basis der Untersuchung ist eine schriftliche Befragung bei 700 männlichen Radiologen; Response 84 % | |
| Maconochie et al. 2001 | 18 131 männliche Beschäftigte in der Atomwirtschaft, vor und nach Beschäftigungsbeginn | Geschlechtsverhältnis (m/w): | ||||||
| N = 20 703 m = 10 622* w = 10 081* * aus Angaben zum Geschlechtsverhältnis geschätzt |
N = 18 799 m = 9 682* w = 9 117* * aus Angaben zum Geschlechtsverhältnis geschätzt |
1,06 vor Beschäftigungsbeginn 1,06 nach Beschäftigungsbeginn |
mit der Allgemeinbevölkerung | kein Unterschied des Geschlechtsverhältnisses vor und nach Beschäftigungsbeginn und im Vergleich zur Allgemeinbevölkerung | ||||
| unterteilt nach Dosisgruppen | N = 23 624 | 1,06 | nicht überwacht | interner Vergleich | kein Zusammenhang zwischen Strahlenexposition und Geschlechtsverhältnis | |||
| N = 3 234 | 1,09 | 0 bis 2,4 mSv | ||||||
| N = 3 582 | 1,11 | 2,5 bis 9,9 mSv | ||||||
| N = 2 397 | 1,06 | 10 bis 19,9 mSv | ||||||
| N = 3 104 | 1,05 | 20 bis 49,9 mSv | ||||||
| N = 3 024 | 1,03 | ≥ 50 mSv | ||||||
| Maconochie et al. 2001 | 4 335 weibliche Beschäftigte in der Atomwirtschaft, vor und nach Beschäftigungsbeginn | N = 2 551 m = 1 301* w = 1 250* * aus Angaben zum Geschlechtsverhältnis geschätzt |
N = 6 326 m = 3 207* w = 3 119* * aus Angaben zum Geschlechtsverhältnis geschätzt |
Geschlechts-verhältnis: 1,03 vor Beschäftigungsbeginn 1,04 nach Beschäftigungsbeginn |
mit der Allgemeinbevölkerung | kein statistisch signifikanter Unterschied des Geschlechtsverhältnisses vor und nach Beschäftigungsbeginn und im Vergleich zur Allgemeinbevölkerung | ||
| unterteilt nach Dosisgruppen | N = 8 076 | 1,03 | nicht überwacht | interner Vergleich | kein Zusammenhang zwischen Strahlenexposition und Geschlechtsverhältnis | |||
| N = 278 | 1,24 | 0 bis 2,4 mSv | ||||||
| N = 275 | 1,07 | 2,5 bis 9,9 mSv | ||||||
| N = 122 | 1,49 | 10 bis 19,9 mSv | ||||||
| N = 82 | 0,78 | 20 bis 49,9 mSv | ||||||
| N = 20 | 1,50 | ≥ 50 mSv | ||||||
| akute Exposition | ||||||||
| Turpin et al. 1956 | Strahlentherapiepatienten ohne Krebserkrankung, die innerhalb der Beckenregion exponiert wurden | Anteil der Jungen: | Verschiebung des Geschlechtsverhältnisses hin zu den Jungen | Basis der Untersuchung ist eine Erhebung; Response bei exponierten Männern: 37,3 %, Zeit zwischen Bestrahlung und Konzeption: 0 bis 8 Jahre | ||||
| Männer: N = 696 m = 358 w = 338 |
vor Behandlung: 0,514±0,019 | vor vs. nach Strahlentherapie | ||||||
| Männer niedrigeDosis: N = 161 m = 85 w = 76 |
nach Behandlung: 0,528±0,039 | < 1 000 r (Ø 721 r) | ||||||
| Männer hohe Dosis: N = 244 m = 140 w = 104 |
nach Behandlung: 0,574±0,032 | > 1 000 r (Ø 1 730 r) | ||||||
| Frauen: N = 136 m = 63 w = 73 |
Frauen: N = 236 m = 130 w = 106 |
vor Behandlung: 0,551±0,034 | vor vs. nach Strahlentherapie | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen | Response bei exponierten Frauen: 33,5 % | |||
| nach Behandlung: 0,463±0,044 | Ø 1 360 r | |||||||
| Lejeune et al. 1960 | Strahlentherapiepatienten ohne Krebserkrankung, die innerhalb der Beckenregion exponiert wurden | Anteil der Jungen: | vor vs. nach Strahlentherapie innerhalb der Beckenregion | Verschiebung des Geschlechtsverhältnisses hin zu den Jungen | Zeit zwischen Bestrahlung und Konzeption: unbekannt | |||
| Männer: N = 656 m = 368 |
Männer: N = 1 185 m = 610 |
vor Behandlung: 0,515±0,015 nach Behandlung: 0,561±0,02 |
1 350 bis 1 700 r Hautdosis |
|||||
| Frauen: N = 161 m = 72 |
Frauen: N = 355 m = 194 |
vor Behandlung: 0,546±0,027 nach Behandlung: 0,447±0,039 |
vor vs. nach Strahlentherapie innerhalb der Beckenregion | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen | ||||
| Strahlentherapiepatienten ohne Krebserkrankung, die außerhalb der Beckenregion exponiert wurden | Männer: N = 1 394 m = 641 |
Männer: N = 1 926 m = 1 015 |
vor Behandlung: 0,527±0,011 nach Behandlung: 0,460±0,014 |
1 275 bis 1 650 r Hautdosis 2 bis 20 r geschätzte Testisdosis |
vor vs. nach Strahlentherapie außerhalb der Beckenregion | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen signifikant | ||
| Frauen: N = 797 m = 416 |
Frauen: N = 647 m = 338 |
vor Behandlung: 0,5014±0,019 nach Behandlung: 0,5219±0,018 |
1 240 bis 1 600 r Hautdosis |
vor vs. nach Strahlentherapie außerhalb der Beckenregion | Veränderung des Geschlechtsverhältnisses nicht signifikant | |||
| Scholte und Sobels 1963 | Strahlentherapiepatienten ohne Krebserkrankung, mit hoher Gonadendosis | Anteil der Jungen in %: | vor vs. nach Exposition Kontrollen vs. Bevölkerungsdurchschnitt |
Paternale Strahlenexposition: Verschiebung des Geschlechtsverhältnisses hin zu den Jungen |
Basis: Krankenhausunterlagen und Standesämter; Zeit zwischen Bestrahlung und Konzeption: unbekannt Männliche Kontrollen (vor Bestrahlung) zeigen eine signifikante Abweichung vom Bevölkerungsdurchschnitt |
|||
| Männer: N = 932 m = 489 |
Männer : N = 1 258 m = 601 |
Kontr. 47,0 % Exp. 52,5 % |
26 bis 500 rad Gonadendosis | |||||
| Frauen: N = 230 m = 112 |
Frauen: N = 242 m = 131 |
Kontr. 54,1 % Exp. 48,5 % |
70 bis 270 rad Gonadendosis | Maternale Strahlenexposition: Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen |
||||
| mit niedriger Gonadendosis | Männer: N = 668 m = 357 |
Männer: N = 657 m = 344 |
Kontr. 52,3 % Exp. 53,3 % |
1 bis 10 rad geschätzte Testisdosis | vor vs. nach Exposition | Paternale Strahlenexposition: Geringfügige Verschiebung des Geschlechtsverhältnisses hin zu den Jungen |
||
| Schull und Neel 1958 | Atombombenüberlebende: Kinder, die zwischen 1948 und 1955 geboren wurden | Anteil der Jungen in %: | 0 bis > 200 rep | Exponierte vs. Nicht-Exponierte mit unterschiedlichen Dosen | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen; Unterschied sehr gering; kein Unterschied zwischen maternaler oder paternaler Exposition |
Zeit zwischen Bestrahlung und Konzeption: unbekannt z. T. elterliche Verwandtschaften mit einbezogen |
||
| Männer: N = 7 525 m = 3 914 w = 3 613 |
Männer: N = 46 166 m = 24 076 w = 22 090 |
Kontr. 52,2 % Exp. 51,7 % |
||||||
| Frauen: N = 27 057 m = 13 990 w = 13 067 |
Frauen: N = 46 166 m = 24 076 w = 22 090 |
Kontr. 52,2 % Exp. 51,7 % |
||||||
| Schull et al. 1966 | Atombomben-überlebende: Kinder, die zwischen 1956 und 1962 geboren wurden | Anteil der Jungen in %: | 0 bis > 200 rep nicht-exponiert und drei Expositionsklassen; Überschätzung wegen T65D | Exponierte vs. Nicht-Exponierte mit unterschiedlichen Dosen | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen; Unterschied sehr gering; kein Unterschied zwischen maternaler oder paternaler Exposition |
Zeit zwischen Bestrahlung und Konzeption: unbekannt; große Studie, Exposition überschätzt, trotzdem hohe Aussagekraft | ||
| Männer N = 7 770 m = 4 009 w = 3 761 |
Männer N = 20 382 m = 10 483 w = 9 944 |
Kontr. 51,4 % Exp. 51,6 % |
||||||
| Frauen: N = 12 562 m = 6 486 w = 6 765 |
Frauen: N = 20 382 m = 10 483 w = 9 944 |
Kontr. 51,4 % Exp. 51,6 % |
||||||
| Neel et al. 1990 | Nachkommen der Atombombenüberlebenden | Keine Neuauswertung der Daten von Schull et al., 1966, trotz neuer Dosimterie, da das frühere Ergebnis nicht für die Hypothese einer Verschiebung des Geschlechtsverhältnisses hin zu den Jungen sprach. | Exponierte vs. Nicht-Exponierte | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen, aber keine absoluten Zahlen angegeben | ||||
| Yoshimoto et al. 1991 | Atombomben-überlebende: Kinder, die zwischen 1946 und 1984 geboren wurden | 40 962 | Anteil der Jungen in %: | mittlere Gonadendosis 0,405 Sv (0,047 Sv Neutronenstrahlung und 0,358 Sv Gammastrahlung) | Exponierte mit unterschiedlichen Dosen | Verschiebung des Geschlechtsverhältnisses hin zu den Mädchen, keine Dosis-Wirkungs-Beziehung | Zeit zwischen Bestrahlung und Konzeption: unbekannt; keine Angabe des Geschlechtsverhältnisses bei Nicht-Exponierten |
|
| Männer N = 7 360 m = 3 609 w = 3 751 |
Exp: 49,0 % | |||||||
| Frauen: N = 12 017 m = 6 154 w = 5 863 |
Exp: 51,2 % | |||||||
| Dickinson et al. 1996 | Sellafield- Beschäftigte |
16 039 Kinder von in Sellafield beschäftigten Vätern | 244 021 Kinder von nicht in Sellafield beschäftigten Vätern | Geschlechts-verhältnis: Kontr. 1,055 |
Vergleichsregion Cumbria; jemals vs. niemalsbeschäftigt |
Verschiebung des Geschlechtsverhältnisses hin zu den Jungen Große Schwankungsbreite in der Bevölkerung, jüngere Väter haben mehr Jungen (1,060) |
große Studie, nur externe Exposition, keine Dosis- Wirkungs-Beziehung für den Vergleich innerhalb der Gruppe der in Sellafield beschäftigten Väter Mögliche Fehler bei Abschätzung der präkonzeptionellen Dosis |
|
| Exp. 1,094 |
0 bis 10 mSv |
|||||||
| 1,396 | > 10 mSv | |||||||
| Mudie et al. 2007 | Kasachstan, Atombomben-Tests | 11 464 Kinder von 3 992 Müttern | Unbekannt; Vergleichsregion: Kasachstan insgesamt | Geschlechtsverhältnis: | Kein Zusammenhang zwischen Strahlenexposition und Geschlechtsverhältnis | kleinere Studie, unzureichende Dosimetrie, keine Dosis-Wirkungs-Beziehung, Auswirkungen der fehlerhaften Dosimetrie nicht abschätzbar | ||
| 1,06 | Kontrollen | |||||||
| 1,04 | < 200 mSv | |||||||
| 1,05 | 200 bis 399 mSv | |||||||
| 1,08 | 400 bis 599 mSv | |||||||
| 1,12 | 600+ mSv | |||||||
- Exp.
-
Exponierte
- Kontr.
-
Kontrollen, nicht exponiert bzw. vor Exposition
- N
-
Gesamtzahl Kinder
- m
-
männlich
- w
-
weiblich
- u
-
unbekanntes Geschlecht
- 1
- Extravariation (oder auch Überdispersion) bedeutet, dass die Varianz des Merkmals „Geschlechtsverhältnis“ größer ist, als aufgrund der Annahme einer Binomialverteilung zu erwarten.
- 2
- Herzschlag, Pulsieren der Nabelschnur und natürliche Lungenatmung (siehe Kapitel 2)
- 3
- Diese Begriffe werden im folgenden Text immer dann verwendet, wenn Aussagen mit regionalen Bezügen getroffen werden. Die Bezeichnungen „DDR“ und „BRD“ werden verwendet, wenn Bezug auf hoheitsrechtliche Regelungen genommen wird.
- 4
- Die Totgeborenenquote beschreibt den Anteil der Totgeburten an der Summe der Lebend- und Totgeburten.
- 5
- Allerdings ist zu berücksichtigen, dass die definitorischen Unterschiede hinsichtlich Totgeborener innerhalb Europas groß sind. Viele Länder ziehen die Schwangerschaftsdauer als Kriterium heran. Dieses Kriterium für eine Totgeburt liegt von Staat zu Staat zwischen 21 und 28 Wochen. Auch das Geburtsgewicht (500 g oder 1 000 g) und die Körperlänge (25 cm, 30 cm oder 35 cm) werden von einigen Staaten herangezogen. Manche Länder wenden gleich mehrere dieser Kriterien an (EC 2003).
- 6
- Das heißt, dass es sich um eine Differenz zwischen Prozentwerten handelt.
- 7
- Extravariation (oder auch Überdispersion) bedeutet, dass die Varianz des Merkmals „Geschlechtsverhältnis“ größer ist als aufgrund der Annahme einer Binomialverteilung zu erwarten.
- 8
- In den entsprechenden Gebietsständen
- 9
- In den entsprechenden Gebietsständen
- 10
- Das Dosimetriesystem, auf das sich die Autoren beziehen, ist T65D (ABCC Technical Report 1-68).
- 11
- Vor dem Hintergrund der erhöhten Leukämiehäufigkeit in Seascale nahe Sellafield und der Ergebnisse der Gardner-Studie (Gardner et al. 1990), die einen Zusammenhang zwischen dem Risiko eines Kindes, an einer Leukämie zu erkranken, und der präkonzeptionellen Strahlenexposition des Vaters in der Anlage Sellafield zeigte, wurden eine Reihe weiterer Untersuchungen durchgeführt, darunter auch die hier referierte von Dickinson et al. (1996).
- 12
- r steht hier für Röntgen oder rad; 1 r entspricht in etwa 0,01 Gy.

